KoreanFoodie's Study
[종만북 문제] 울타리 잘라내기 (문제 ID : FENCE, 난이도 : 중) 본문
Data Structures, Algorithm/종만북
[종만북 문제] 울타리 잘라내기 (문제 ID : FENCE, 난이도 : 중)
GoldGiver 2024. 3. 5. 20:51
프로그래밍 대회에서 배우는 알고리즘 문제해결 전략(이하 종만북)에서 소개된 문제를 풀이합니다. 알고리즘에 진심이시라면, 직접 구매하셔서 읽어보시는 것을 추천합니다!
핵심 :
1. 분할 조건을 잘 따져보자.
[종만북 문제] 울타리 잘라내기 (문제 ID : FENCE, 난이도 : 중)
이 문제는 아래처럼 무식하게 풀면 O(N^2) 에 풀 수는 있지만, 시간초과가 난다. 😅

이를 해결하기 위해, 우리는 분할 정복을 사용할 것이다.

(c) 가 조금 까다로워 보일 수 있는데... 핵심은, 걸쳤을 경우 해당 판자를 반드시 포함한다는 것이다!
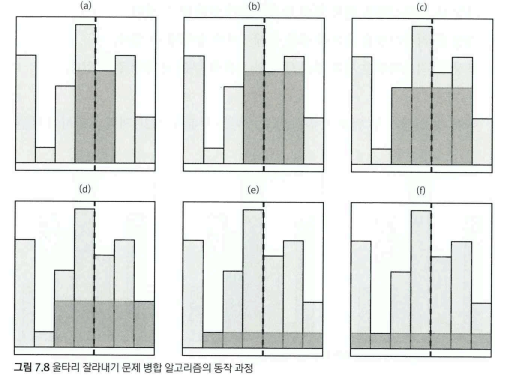
즉, (a) 에서부터 시작한다고 가정하자. 판자의 왼쪽과 오른쪽 중, 우리는 더 높이가 큰 것을 택한다. 고로 (b) 에서 오른쪽이 선택된다. 다시 (b) 에서는 왼쪽과 오른쪽 판자 중 높은 것을 선택해야 하므로, 왼쪽이 선택되어 (c) 처럼 판자가 확장될 것이다!
소스 코드는 아래와 같다. 😌
#include <iostream>
#include "stdlib.h"
#include <vector>
#include <cmath>
using namespace std;
int N;
vector<int> h;
// [left ~ right] 구간에서 찾아낼 수 있는 가장 큰 사각형의 넓이 반환
int sol(int left, int right)
{
// 기저 사례 : 판자가 하나밖에 없음
if (left == right) return h[left];
// [left, mid], [mid + 1, right] 두 구간으로 문제 분할
int mid = (left + right) / 2;
// 각개격파
int ans = max(sol(left, mid), sol(mid + 1, right));
// 부분 문제 3 : 두 부분에 모두 걸치는 사각형 중 가장 큰 것을 찾는다
int lo = mid, hi = mid + 1;
int height = min(h[lo], h[hi]);
// [mid, mid+1] 만 포함하는 너비 2인 사각형 고려
ans = max(ans, height * 2);
// 사각형이 입력 전체를 덮을 때까지 확장
while (left < lo || hi < right)
{
// 항상 높이가 더 높은 쪽으로 확장
if (hi < right && (lo == left || h[lo - 1] < h[hi + 1]))
{
++hi;
height = min(height, h[hi]);
}
else
{
--lo;
height = min(height, h[lo]);
}
// 확장한 후 사각형의 넓이
ans = max(ans, height * (hi - lo + 1));
}
return ans;
}
void inputHandler()
{
cin >> N;
h.clear();
h.resize(N);
for (int i = 0; i < N; ++i)
cin >> h[i];
}
int main()
{
int cases;
cin >> cases;
while (cases--)
{
inputHandler();
cout << sol(0, N-1) << endl;
}
return 0;
}'Data Structures, Algorithm > 종만북' 카테고리의 다른 글
| [종만북 문제] 외발 뛰기 (문제 ID : JUMPGAME, 난이도 : 하) (0) | 2024.03.08 |
|---|---|
| [종만북 문제] 팬미팅 (문제 ID : FANMEETING, 난이도 : 상) (1) | 2024.03.06 |
| [종만북 문제] 쿼드 트리 뒤집기 (문제 ID : QUADTREE, 난이도 : 하) (0) | 2024.03.05 |
| [종만북 문제] Synchronizing Clocks, 시계 맞추기 (문제 ID : CLOCKSYNC, 난이도 : 중) (0) | 2024.03.04 |
| [종만북 문제] 게임판 덮기 (문제 ID : BOARDCOVER, 난이도 : 하) (0) | 2024.03.04 |
Comments




