KoreanFoodie's Study
딥러닝 튜토리얼 6-2강, 배치 정규화, 오버피팅, 하이퍼 파라미터 최적화 - 밑바닥부터 시작하는 딥러닝 본문
딥러닝 튜토리얼 6-2강, 배치 정규화, 오버피팅, 하이퍼 파라미터 최적화 - 밑바닥부터 시작하는 딥러닝
GoldGiver 2020. 2. 1. 09:42
해당 포스팅은 한빛 미디어에서 출판한 '밑바닥부터 시작하는 딥러닝'이라는 교재의 내용을 따라가며 딥러닝 튜토리얼을 진행하고 있습니다. 관련 자료는 여기에서 찾거나 다운로드 받으실 수 있습니다.
배치 정규화
이전 포스팅에서, 가중치의 초깃값을 적절히 설정하면 각 층의 활성화값 분포가 적당히 퍼지면서 학습이 원활하게 수행됨을 배웠다. 그렇다면 각 층이 활성화를 적당히 퍼뜨리도록 '강제'할 수도 있을까? 실은 배치 정규화(Batch Normalization)가 그런 아이디어에서 출발한 방법이다!
-
배치 정규화 알고리즘
배치 정규화는 2015년에 나온 기법임에도 널리 사용되고 있는 방식이다. 배치 정규화가 주목받는 이유는 다음과 같다.
- 학습을 빨리 진행할 수 있다(학습 속도 개선).
- 초깃값에 크게 의존하지 않는다(골치 아픈 초깃값 선택 장애여 안녕!).
- 오버피팅을 억제한다(드롭아웃 등의 필요성 감소).
배치 정규화의 기본 아이디어는 앞에서 말했듯이 각 층에서의 활성화값이 적당히 분포되도록 조정하는 것이다. 그래서 아래 그림과 같이 데이터 분포를 정규화하는 '배치 정규화 계층(Batch Norm)'을 신경망에 삽입한다.

배치 정규화는 그 이름과 같이 학습 시 미니배치를 단위로 정규화한다. 구체적으로는 데이터 분포가 평균이 0, 분산이 1이 되도록 정규화한다. 수식으로는 다음과 같다.

여기에는 미니배치 B = {x1, x2, ... xm}이라는 m개의 입력 데이터의 집합에 대해 평균과 분산을 구한다. 그리고 입력 데이터를 평균이 0, 분산이 1이 되게(적절한 분포가 되게) 정규화한다. 그리고 입실론 값은 작은 값(예를 들어 10e-7)으로, 0으로 나누는 사태를 예방하는 역할이다.
위 식은 단순히 미니배치 입력 데이터를 평균 0, 분산 1인 데이터로 변환하는 일을 한다. 이 처리를 활성화 함수의 앞(혹은 뒤)에 삽입함으로써 데이터 분포가 덜 치우치게 할 수 있다.
또, 배치 정규화 계층마다 이 정규화된 데이터에 고유한 확대(scale)와 이동(shift) 변환을 수행한다. 수식으로는 다음과 같다!

이 식에서 γ(감마)는 확대를, β(베타)가 이동을 담당한다. 두 값은 처음에는 1, 0부터 시작하고, 학습하면서 적합한 값으로 조정해 간다.
이상이 배치 정규화의 알고리즘이다. 이 알고리즘이 신경망에서 순전파 때 적용된다. 이를 5장에서 설명한 계산 그래프로는 다음과 같이 그릴 수 있다.
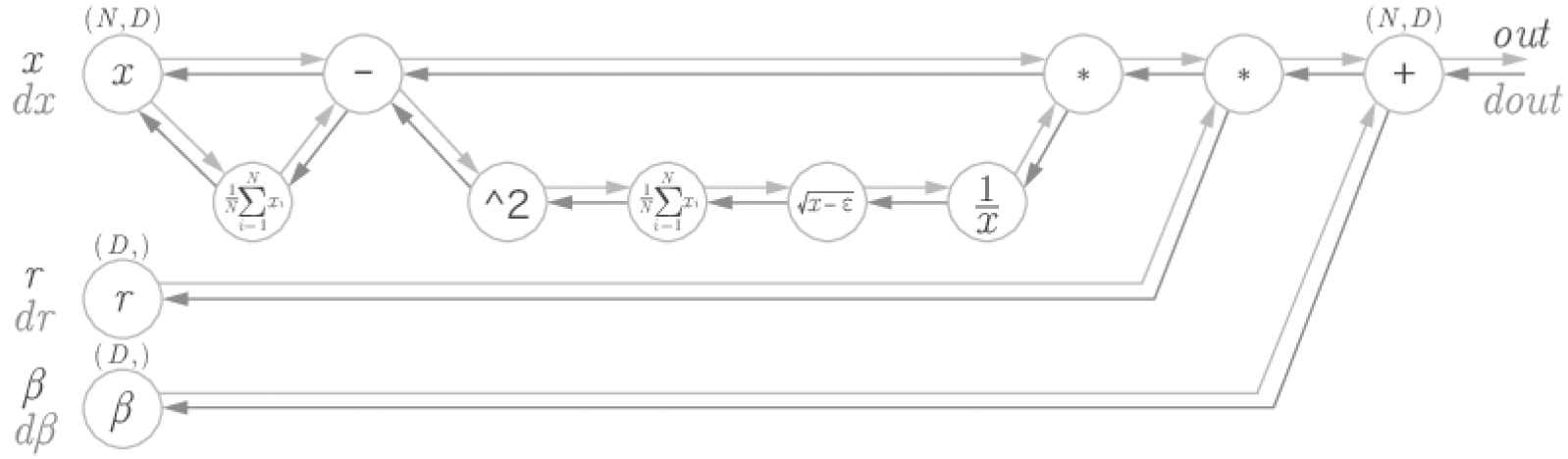
자세한 설명은 프레드릭 크레저트(Frederik Kratzert)의 블로그에서 찾을 수 있다!
-
배치 정규화의 효과
그럼 배치 정규화 계층을 사용한 실험을 해 보자. 우선은 MNIST 데이터셋을 사용하여 배치 정규화 계층을 사용할 때와 사용하지 않을 때의 학습 진도가 어떻게 달라지는지를 보자! (소스 코드는 ch06/batch_norm_test.py에 있다.)

위 그림과 같이 배치 정규화가 학습을 빨리 진전시키고 있다. 계속해서 초깃값 분포를 다양하게 줘가며 학습 진해잉 어떻게 달라지는지를 보자. 아래 그림은 가중치 초깃값의 표준편차를 다양하게 바꿔가며 학습 경과를 관찰한 그래프이다.
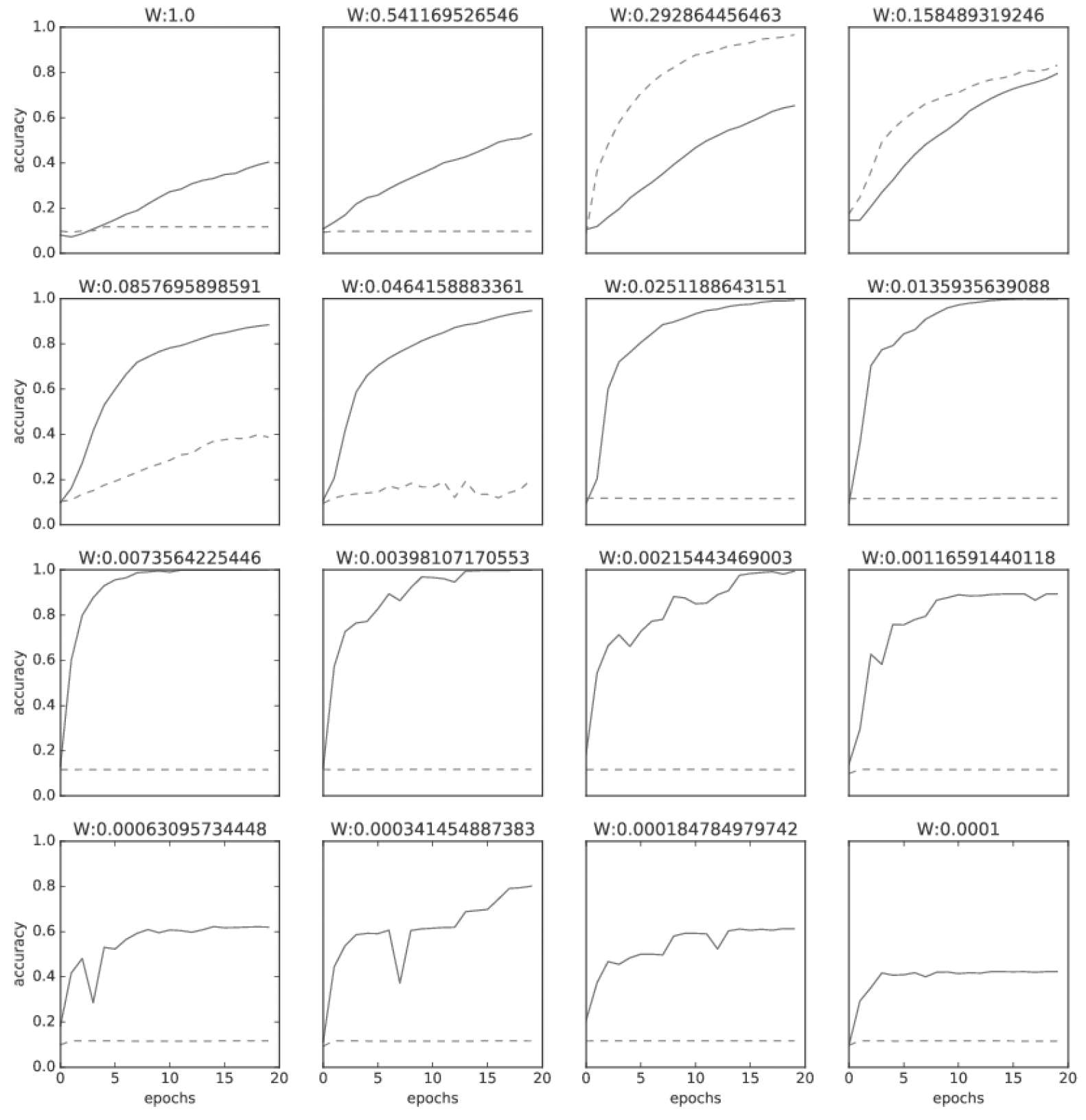
거의 모든 경우에서 배치 정규화를 사용할 때의 학습 진도가 빠른 것으로 나타난다. 실제로 배치 정규화를 사용하지 않는 경우엔 초깃값이 잘 분포되어 있지 않으면 학습이 전혀 진행되지 않는 모습도 확인할 수 있다!
지금까지 살펴본 것처럼 배치 정규화를 사용하면 학습이 빨라지며, 가중치 초깃값에 크게 의존하지 않아도 된다. 배치 정규화는 이처럼 장점이 많으니 앞으로 다양한 분야에서 활약할 것이다!
오버피팅
기계학습에서는 오버피팅이 문제가 되는 일이 많다. 오버피팅이란 신경망이 훈련 데이터에만 지나치게 적응되어 그 외의 데이터에는 제대로 대응하지 못하는 상태를 의미한다.
-
오버피팅
오버피팅은 주로 다음의 두 경우에 일어난다.
1. 매개변수가 많고 표현력이 높은 모델
2. 훈련 데이터가 적음
이번 포스팅에서는 이 두 요건을 일부러 충족하여 오버피팅을 일으켜 보겠다. 그러기 위해 MNIST 데이터셋의 훈련 데이터 중 300개만 사용하고, 7층 네트워크를 사용해 네트워크의 복잡성을 높이겠다. 각 층의 뉴런은 100개, 활성화 함수는 ReLU를 사용한다(소스 코드는 ch06/overfit_weight_decay.py에 있다).
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
# 오버피팅을 재현하기 위해 학습 데이터 수를 줄인다
x_train = x_train[:300]
t_train = t_train[:300]이어서 훈련을 수행하는 코드이다. 지금까지의 코드와 같지만, 에폭마다 모든 훈련 데이터와 모든 시험 데이터 각각에서 정확도를 산출한다!
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
optimizer = SGD(lr = 0.01) # 학습률이 0.01인 SGD로 매개변수 갱신
max_epochs = 201
train_size = x_train.shape[0]
batch_size = 100
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
epoch_cnt = 0
for i in range(100000000):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
grads = network.gradient(x_batch, t_batch)
optimizer.update(network.params, grads)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
epoch_cnt += 1
if epoch_cnt >= max_epochs:
break

훈련 데이터를 사용하여 측정한 정확도는 100 에폭을 지나는 무렵부터 거의 100%이다. 그러나 시험 데이터에 대해서는 큰 차이를 보인다! 이처럼 정확도가 크게 벌어지는 것은 훈련 데이터에만 적응(fitting)해버린 결과이다. 훈련 때 사용하지 않은 범용 데이터(시험 데이터)에는 제대로 대응하지 못하는 것을 이 그래프에서 확인할 수 있다.
-
가중치 감소
오버피팅 억제용으로 예로부터 많이 이용해온 방법 중 가중치 감소(weight decay)라는 것이 있다. 이는 학습 과정에서 큰 가중치에 대해서는 그에 상응하는 큰 페널티를 부과하여 오버피팅을 억제하는 방법이다. 원래 오버피팅은 가중치 매개변수의 값이 커서 발생하는 경우가 많기 때문이다.
자 복습해보자. 신경망 학습의 목적은 손실 함수의 값을 줄이는 것이다. 이때, 예를 들어 가중치의 제곱 노름(norm, L2 노름)을 손실 함수에 더한다. 그러면 가중치가 커지는 것을 억제할 수 있다. 가중치를 W라고 하면 L2 노름에 따른 가중치 감소는 1/2 * λ * W^2이 되고, 이 1/2 * λ * W^2을 손실 함수에 더한다. 여기서 λ(람다)는 정규화의 세기를 조절하는 하이퍼파라미터이다. λ를 크게 설정할수록 큰 가중치에 대한 페널티가 커진다. 또 앞쪽 1/2은 1/2 * λ * W^2의 미분 결과인 λ * W를 조정하는 역할의 상수이다.
가중치 감소는 모든 가중치 각각의 손실 함수에 1/2 * λ * W^2 값을 더한다. 따라서 가중치의 기울기를 구하는 계산에서는 그동안의 오차역전파법에 따른 결과에 정규화 항을 미분한 λ * W 값을 더한다.
L2 노름은 각 원소의 제곱들을 더한 것에 해당한다. 가중치 W = (w1, w2, ... ,wn)이 있다면, L2 노름에서는 sqrt(w1^2 + w2^2 + ... + wn^2) 으로 계산할 수 있다. L2 노름 외에 L1 노름과 L(Inf)노름도 있다. L1 노름은 절댓값의 합, 즉 |w1| + |w2| + ... + |wn|에 해당한다. L(inf) 노름은 Max 노름이라고도 하며, 각 원소의 절댓값 중 가장 큰 것에 해당한다. 정규화 항으로 L2 노름, L1 노름, L(inf) 노름 중 어떤 것도 사용할 수 있다.
그럼 실험을 해 보자. 방금 수행한 실험에서 λ = 0.1로 가중치 감소를 적용한다. 코드는 common/multi_layer_net.py에, 실험용 코드는 ch06/overfit_weight_decay.py에 있다!

위 그림을 보면, 오버피팅이 어느 정도 억제되었음을 확인해 볼 수 있다!
-
드롭아웃
앞 절에서는 오버피팅을 억제하는 방식으로 손실 함수에 가중치의 L2 노름을 더한 가중치 감소 방법을 설명했다. 가중치 감소는 간단하게 구현할 수 있고, 어느 정도 지나친 학습을 엊게할 수 있다. 그러나 신경망 모델이 복잡해지면 가중치 감소만으로는 대응하기 어려워진다. 이럴 때는 흔히 드롭아웃(Dropout)이라는 기법을 이용한다.
드롭아웃은 뉴런을 임의로 삭제하면서 학습하는 방법이다. 훈련 때 은닉층의 뉴런을 무작위로 골라 삭제한다. 삭제된 뉴런은 아래 그림과 같이 신호를 전달하지 않게 된다. 훈련 때는 데이터를 흘릴 때마다 삭제할 뉴런을 무작위로 선택하고, 시험 때는 모든 뉴런에 신호를 전달한다. 단, 시험 때는 각 뉴런의 출력에 훈련 때 삭제한 비율을 곱하여 출력한다.

이제 드롭아웃을 구현해 보자. 순전파를 담당하는 forward 메서드에서는 훈련 때(train_flg = True일 때)만 잘 계산해두면 시험 때는 단순히 데이터를 흘리기만 하면 된다. 삭제한 비율은 곱하지 않아도 좋다. 실제 딥러닝 프레임워크들도 비율을 곱하지 않는다! 더 효율적인 구현이 궁금하면 체이너(Chainer) 프레임워크(http://chainer.org/)의 드롭아웃 구현을 참고해 보자.
class Dropout:
def __init__(self, dropout_ratio=0.5):
self.dropout_ratio = dropout_ratio
self.mask = None
def forward(self, x, train_flg=True):
if train_flg:
self.mask = np.random.rand(*x.shape) > self.dropout_ratio
return x * self.mask
else:
return x * (1.0 * self.dropout_ratio)
def backward(self, dout):
return dout * self.mask여기에서의 핵심은 훈련 시에는 순전파 때마다 self.mask에 삭제할 뉴런을 False로 표시한다는 것이다. self.mask는 x와 형상이 같은 배열을 무작위로 생성하고, 그 값이 dropout_ratio보다 큰 원소만 True로 설정한다. 역전파 때의 동작은 ReLU와 같다. 즉, 순전파 때 신호를 통과시키는 뉴런은 역전파 때도 신호를 그대로 통과시키고, 순전파 때 통과시키지 않은 뉴런은 역전파 때도 신호를 차단한다.
그럼 드롭아웃의 효과를 MNIST 데이터셋으로 확인해 보자. 소스코드는 ch06/overfit_dropout.py에 있다.

왼쪽은 드롭아웃 없이, 오른쪽은 드롭아웃을 적용한 결과이다. 이처럼, 드롭아웃을 이용하면 표현력을 높이면서도 오버피팅을 억제할 수 있다!
기계학습에서는 앙상블 학습(Ensenble learning)을 애용한다. 앙상블 학습은 개별적으로 학습시킨 여러 모델의 출력을 평균 내어 추론하는 방식이다. 신경망의 맥락에서 얘기하면, 가령 같은 (혹은 비슷한) 구조의 네트워크를 5개 준비하여 따로따로 학습시키고, 시험 때는 그 5개의 출력을 평균 내어 답하는 것이다. 앙상블 학습을 수행하면 신경망의 정확도가 몇% 정도 개선된다는 것이 실험적으로 알려져 있다.
앙상블 학습은 드롭아웃과 밀접하다. 드롭아웃이 학습 때 뉴런을 무작위로 삭제하는 행위를 매번 다른 모델을 학습시키는 것으로 해석할 수 있기 때문이다. 그리고 추론 때는 뉴런의 출력에 삭제한 비율(이를테면 0.5등)을 곱함으로써 앙상블 학습에서 여러 모델의 평균을 내는 것과 같은 효과를 얻는 것이다. 즉, 드롭아웃은 앙상블 학습과 같은 효과를(대략) 하나의 네트워크로 구현했다고 생각할 수 있다!
적절한 하이퍼파라미터 값 찾기
모델의 성능을 개선하기 위해, 적절한 하이퍼파라미터 값을 찾는 것은 매우 중요하다. 다만, 하이퍼파라미터의 성능을 평가할 때는 시험 데이터를 사용하면 안된다! 하이퍼파라미터의 성능을 평가할 때 시험 데이터를 이용하면, 모델이 시험 데이터에 오버피팅될 수 있기 때문이다!
그래서 하이퍼 파라미터를 조정할 때에는 하이퍼 파라미터 전용 확인 데이터가 필요한데, 이를 일반적으로 검증 데이터(Validation data)라고 부른다. 검증데이터를 얻는 가장 간단한 방법은 시험 데이터에서 일부(예를 들어 20%)를 추출하는 것이다.
-
하이퍼파라미터 최적화
하이퍼파라미터를 최적화할 때의 핵심은 하이퍼파라미터의 '최적 값'이 존재하는 범위를 조금씩 줄여간다는 것이다. 범위를 조금씩 줄이려면 우선 대략적인 범위를 설정하고 그 범위에서 무작위로 하이퍼파라미터 값을 골라낸(샘플링) 후, 그 값으로 정확도를 평가한다. 정확도를 잘 살피면서 이 작업을 여러 번 반복하며 하이퍼파라미터의 '최적 값'의 범위를 좁혀가는 것이다.
신경망의 하이퍼파라미터 최적화에서는 그리드 서치(Grid search)같은 규칙적인 탐색보다는 무작위로 샘플링해 탐색하는 편이 좋은 결과를 낸다고 알려져 있다. 이는 최종 정확도에 미치는 영향력이 하이퍼파라미터마다 다르기 때문이다!
하이퍼파라미터의 범위는 '대략적으로' 지정하는 것이 효과적이다. 실제로도 0.001에서 1000사이와 같이 '10의 거듭제곱' 단위로 범위를 지정한다. 이를 '로그 스케일로 지정'한다고 한다.
하이퍼파라미터를 최적화할 때는 딥러닝 학습에는 오랜 시간(예컨대 며칠이나 몇 주 이상)이 걸린다는 점을 기억해야 한다. 따라서 나쁠 듯한 값은 일찍 포기하는 게 좋다. 그래서 학습을 위한 에폭을 작게 하여, 1회 평가에 걸리는 시간을 단축하는 것이 효과적이다. 정리하면 다음과 같다!
- 0단계
하이퍼 파라미터 값의 범위를 설정한다
- 1단계
설정된 범위에서 하이퍼파라미터의 값을 무작위로 추출한다.
- 2단계
1단계에서 샘플링한 하이퍼파라미터 값을 사용하여 학습하고, 검증 데이터로 정확도를 평가한다(단, 에폭은 작게 설정한다).
- 3단계
1단계와 2단계를 특정 횟수(100회 등) 반복하며, 그 정확도의 결과를 보고 하이퍼파라미터의 범위를 좁힌다.
여기에서 설명한 하이퍼파라미터 최적화 방법은 실용적인 방법이다. 하지만 과학이라기보다는 다분히 수행자의 직관에 의존한다. 더 세련된 기법을 원한다면 베이즈 최적화(Bayesian Optimization)을 알아보자. 베이즈 최적화는 베이즈 정리를 중심으로 한 수학이론을 구사하여 더 엄밀하고 효율적으로 최적화를 수행한다. 자세한 내용은 <Practical Bayesian Optimization of Machine Learning Algoritms> 논문 등을 참고하자!
-
하이퍼파라미터 최적화 구현하기
이제 실제로 구현을 해 보자.
weight_decay = 10 ** np.random.uniform(-8, -4)
lr = 10 ** np.random.uniform(-6, -2)위 예시는 각각 가중치 감소 계수와 학습률을 조정한 것이다. 이렇게 무작위로 추출한 값을 이용하여 학습을 수행한다. 자세한 구현은 ch06/hyperparameter_optimization.py 파일을 참고하자!

위 결과를 보면 Best-5까지는 대략 학습이 잘 진행되는 것을 알 수 있다.
val acc:0.83 | lr:0.007930777133653748, weight decay:4.285774741857826e-08
val acc:0.08 | lr:2.622049738234655e-06, weight decay:4.940041697515601e-06
val acc:0.49 | lr:0.001976012154057031, weight decay:1.407891931740619e-08
val acc:0.07 | lr:2.059835391667847e-05, weight decay:1.4266563733468448e-06
val acc:0.56 | lr:0.004430642268141839, weight decay:3.5664565404497015e-05
val acc:0.13 | lr:0.00010846540334534612, weight decay:5.388291372869288e-05
val acc:0.15 | lr:0.000416250351827967, weight decay:1.9089887539335125e-06
val acc:0.14 | lr:1.5146890150683426e-06, weight decay:9.314904481576831e-05
val acc:0.83 | lr:0.006912744489471699, weight decay:9.73346368878762e-08실제 코드를 돌리면 아래와 같이 나오며, 정확도가 높은 경우의 학습률 값과 가중치 감소율 값을 택하면 된다!
'Deep Learning > 밑바닥부터 시작하는 딥러닝 1' 카테고리의 다른 글
| 딥러닝 튜토리얼 7-1강, 합성곱 신경망(CNN)의 개념 - 밑바닥부터 시작하는 딥러닝 (0) | 2020.03.08 |
|---|---|
| 딥러닝 튜토리얼 6-1강, SGD, 모멘텀, AdaGrad, Adam, 가중치 초기값 설정 - 밑바닥부터 시작하는 딥러닝 (4) | 2020.01.28 |
| 딥러닝 튜토리얼 5강 2부, 활성화 함수 계층 구현, Affine/Softmax 계층 구현, 오차역전파법 구현 - 밑바닥부터 시작하는 딥러닝 (0) | 2019.12.26 |
| 딥러닝 튜토리얼 5강 1부, 오차역전파법, 계산 그래프 - 밑바닥부터 시작하는 딥러닝 (0) | 2019.11.22 |
| 딥러닝 튜토리얼 4강 2부, 수치 미분과 학습 알고리즘 - 밑바닥부터 시작하는 딥러닝 (0) | 2019.11.07 |




