[OpenGL ES] 2강 : 벡터의 내적/외적, 선형 보간(Linear Interpolation)

이 강의는 유투브에 무료로 공개되어 있는 한정현 교수님의 컴퓨터 그래픽스 강좌를 정리한 글입니다. 자세한 내용은 강의를 직접 들으시거나 책을 구입하셔서 확인해 보세요. 강의 자료는 깃헙 링크에 올라와 있습니다.

---

요약 :

1. 좌표계는 Orthonormal 한 기저 벡터로 정의할 수 있다.

2. 벡터를 내적하면 절댓값에 코사인 값을 곱한 결과가 나온다. 90 도일 경우 0 이다!

3. 외적의 경우, 오른손 법칙으로 방향을 구할 수 있다. 외적의 절댓값은 두 벡터가 만드는 평행사변형의 넓이이다.

좌표계 (Coordinate System and Basis) 와 벡터의 내적/외적

좌표계는 원점(origin)과 기저(basis) 로 이루어진다. 위의 그림에는 2D 공간을 이루는 기저 벡터의 조합이 나와 있는데, 그 중 orthonomal basis 를 자주 이용하게 될 것이다. orthonormal basis 는 orthogonal(직교) 하면서 normalized(크기가 1인)된 기저 벡터를 의미한다.

 

위와 같이 e1, e2, e3 벡터 3개가 있으면 3차원 공간을 표현할 수 있다.

 

벡터의 내적은 이미 배웠으니, 벡터 a 와 b 의 내적은 간단히 ||a|| ||b|| cosθ 로 표현할 수 있다는 것을 알 것이다. 한 가지 기억해야 할 것은, θ 의 크기에 따라 내적값의 부호가 바뀐다는 것이다. θ 가 90도이면 0, θ 가 예각이면 양수, θ 가 둔각이면 음수가 될 것이다.

 

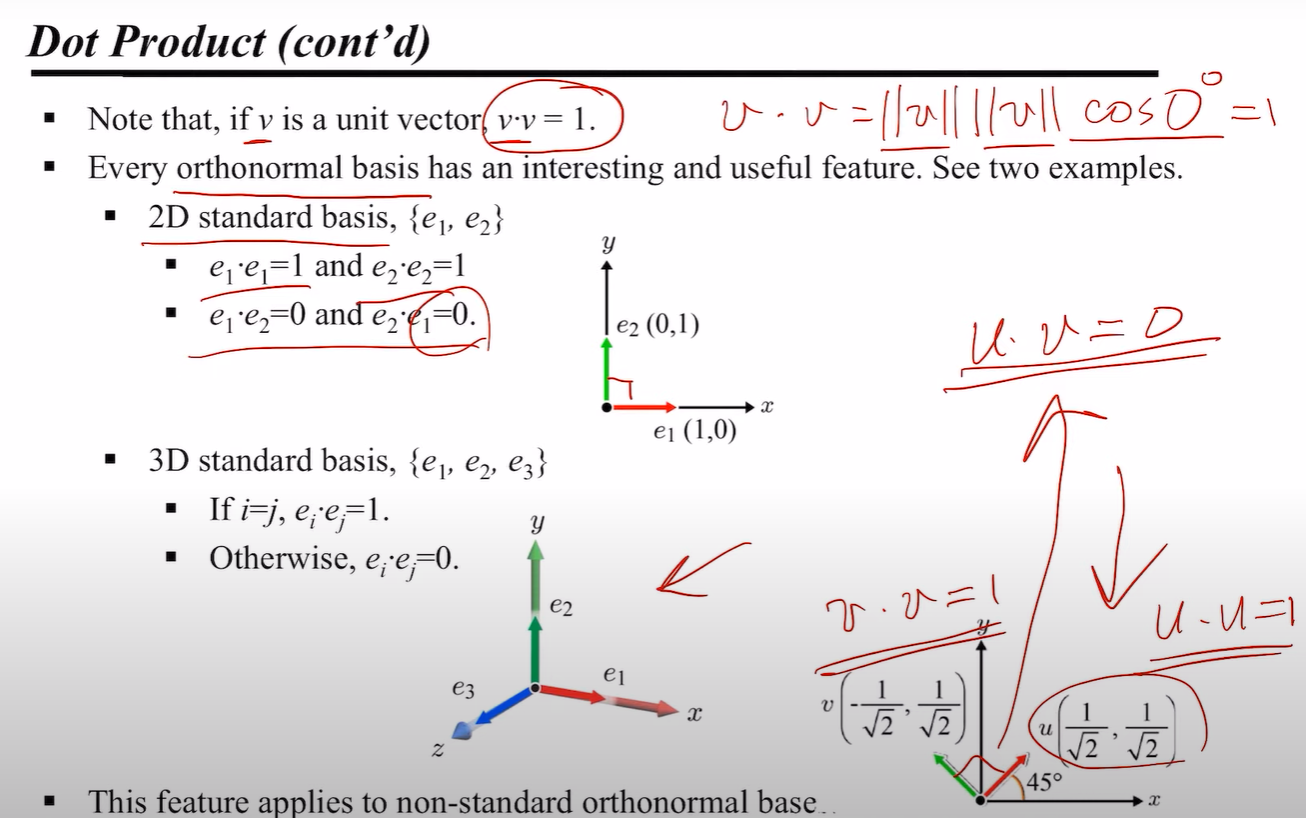
한 가지 더 재미있는 성질은, 기저 벡터끼리의 곱이 같은 녀석일 때는 1, 아닐 때는 0이 나온다는 사실이다. 이는 non-standard 한 orthonormal base 에서도 동일하게 적용되는 성질이다.

 

이제 외적으로 넘어오자. 벡터 a 와 b 에 외적을 취하면, a 와 b 에 직교하는 벡터 a x b 를 구할 수 있다. 이때, 해당 벡터의 방향은 오른손 법칙에 의해 정의된다.

위에서는 a x b 이므로, a 에서 b 쪽으로 손바닥을 감듯이 그러쥐면, 엄지손가락이 향하는 방향이 바로 a x b 가 된다.

a x b 의 길이는 a 와 b 가 만드는 평행사변형의 넓이와 같으며, ||a|| ||b|| sinθ 로 정의된다. 참고로, b x a = - a x b 이다(방향이 반대라는 뜻).

위키피디아에 나온 외적 애니메이션

 

참고로, 외적의 계산식은 위와 같다. 저 반시계 방향의 곱셈 방향만 기억해 두도록 하자.

 

 

Line, Ray, and Linear Interpolation

이름은 거창하지만 사실 직선, 반직선, 그리고 선형 보간에 대한 부분이다.

임의의 직선 위의 두 점 p0 와 p1 이 있다고 했을 때, p(t) 라는 식을 p0 + t(p1 - p0) 로 정의함으로써 우리는 p0 와 p1 사이에 있는 모든 점에 대한 식을 세울 수 있다.

만약 t 의 범위가 -∞ 에서 ∞ 까지라면 p(t) 는 직선(Line)이, 0 에서 ∞ 까지라면 p(t) 는 반직선(ray)이 된다.

마지막으로 t 가 0 에서 1 사이라면 p(t) 는 선분(Line segment)이 될 것이다. 이러한 경우를 linear interpolation(선형 보간)이라고 부른다.

 

위 그림을 보면, 선형 보간을 이용해 3차원 공간에서의 점을 어떻게 표현하는지를 엿볼 수 있다.

또한 좌표 뿐만이 아니라, 색상값의 경우에도 마찬가지의 원리로 보간이 가능하다. 만약 t 가 0.5 라면, 위의 색상 스펙트럼에서 중간에 있는 값을 가져갈 것이다!