KoreanFoodie's Study
[OpenGL ES] 4-2강 : 월드 공간, 오브젝트 공간, 오일러 변환, 임의의 축에 대한 회전 본문
[OpenGL ES] 4-2강 : 월드 공간, 오브젝트 공간, 오일러 변환, 임의의 축에 대한 회전
GoldGiver 2023. 4. 12. 13:25
이 강의는 유투브에 무료로 공개되어 있는 한정현 교수님의 컴퓨터 그래픽스 강좌를 정리한 글입니다. 자세한 내용은 강의를 직접 들으시거나 책을 구입하셔서 확인해 보세요. 강의 자료는 깃헙 링크에 올라와 있습니다.
요약 :
1. 오브젝트 공간에서 정의된 물체는 아핀 변환을 이용해 월드 공간 좌표계에서 표현할 수 있다. 이를 World Transform 이라고 부른다.
2. 오브젝트 공간의 축 u, v, n 을 월드 공간의 축 x, y, z 로 맞춰주려면, u, v, n 을 Transpose 시킨 행렬을 기존 오브젝트 축 행렬에 곱해 주면 된다.
3. 임의의 축에 대한 행렬도 2번과 마찬가지로 진행하면, 좌표계 시스템을 쉽게 변환할 수 있다!
월드 공간과 오브젝트 공간

오브젝트가 정의된 좌표계 시스템을 우리는 '오브젝트 공간'이라고 부른다. 특정 모델의 오브젝트 공간은 다른 모델의 오브젝트 공간과 아무 관련성이 없다.
하지만 실제로 오브젝트는 다른 오브젝트와 함께 씬에 배치되게 된다. 씬에서 사용하는 단일한 좌표계 시스템을 바로 '월드 공간' 이라고 부른다. 따라서 우리는 오브젝트 공간에서 정의된 좌표계 시스템을 월드 공간에서 사용하는 좌표계로 변환해야 한다(그래야 위치 등을 파악할 수 있으니까).

위 그림은 오브젝트 공간에 있던 주전자를 월드 공간으로 변환하는 과정을 보여주고 있다.

우리가 2D 공간에서 정의했던 아핀변환은, 3D 공간에서도 그 원리는 동일하게 동작한다. 다만 차이가 있다면, 행렬의 크기가 4 x 4 라는 것 정도일 것이다.

이전에 했던 것처럼, 3D 아핀 변환에서도 [L|t] 를 만들 수 있다.
오브젝트 공간과 월드 공간 변환

오브젝트가 생성되면, 해당 오브젝트는 오브젝트 공간에 고정된다. 초기에, 오브젝트 공간은 월드 공간과 일치한다(basis 들이 같으니까).
그런데 만약 회전이 적용되면, 오브젝트 공간의 basis 들이 회전되는 것처럼 변동이 발생하게 된다.

위 그림처럼, y 축을 기준으로 주전자를 90 도 회전시킨다고 가정하자. 그럼 회전 행렬 R 을 어떻게 구할 수 있을까?
일단, 우리는 3 x 3 행렬에서 각 열이 오브젝트 공간에서의 basis 벡터를 상징한다는 것을 파악할 수 있다. 각각의 열은 기본적으로 u, v, n 이 될 것이다!
회전행렬을 적용하면, Ry 가 위의 행렬처럼 표현되는데, 이는 오브젝트 공간의 새로운 basis 로서 사용될 것이다.

위에서 관찰한 결과는 축에 한정된 회전뿐만 아니라 임의의 축에 대한 회전에서도 동일하게 적용될 수 있다.
역변환 (Inverse of Translation, Scaling and Rotation)

Translation 을 역으로 만들면, 음수 부호만 붙여주면 된다.
Scaling 의 경우에는, Scaling Factor 에 역수를 취해주면 된다!

그렇다면 회전은 어떨까? 회전의 경우, Transpose 를 취한 행렬을 회전 행렬 앞에 곱하면 Identity Matrix 를 얻을 수 있는 놀라운 성질이 있다. 이것이 가능한 이유는, basis 들이 orthonormal 하기 때문이다!
즉, 회전 행렬의 역행렬이 회전 행렬에 Transpose 를 취한 것이라는 것이다.

그러므로 회전행렬의 역행렬은 위처럼, u, v, n 으로 정의된 기저 벡터를 Transpose 시킴으로써 간단히 구할 수 있다!

주전자 끝에 있는 (0, 2, 3) 점을 보자. 주전자를 회전시켜도, 해당 점이 오브젝트 공간에서 점유하는 상대적 위치는 보존되어야 한다(왜냐면 주전자 자체가 일그러지는 것은 아니니까. 더 정확히 말하면, 강체 변환이니까!).
하지만 해당 점은 월드 공간에서는 분명 좌표가 바뀔 것이다. 그렇다면 해당 변환은 어떻게 진행되는 것일까?
일단 한 가지 명심할 것은 다음과 같다 : 회전행렬 R 은 오브젝트 공간의 벡터들을 월드 공간으로 변환하고, R 의 역행렬은 그 반대의 역할을 수행한다는 것이다.
(0, 0, 0) 에서 (0, 2, 3) 으로 가는 벡터 w 를 정의하자. 이제 해당 벡터에 R 을 곱하면 월드 공간에서의 w 의 값을 알 수 있다.
마찬가지로, 오브젝트 공간의 basis (u, v, n) 에 대해서도 R 을 곱하면... w 는 오브젝트 공간(변환된 u, v, n)에 대해서는 상대적 위치가 보존될 것이다.
물론, 월드 공간에서는 R 을 곱했으니 월드 공간에서의 값은 기존 값 (0, 2, 3) 과는 다른 값이 나올 것이다!

우리는 이전에 임의의 점을 2D 회전시켰다. 이번에는 벡터 p 를 2개의 orthonormal 한 벡터 a, b 를 따라 scaling 을 한다고 해 보자.
그럼, 먼저 해당 점을 a, b 벡터가 만드는 공간으로 변환(편입시킨다고 이해하면 된다)해야 한다. 이를 위해 (3) 번 바로 아래 있는 a, b 열벡터로 이루어진 행렬식을 p 에 곱한다.
그 후, scaling factor 에 맞는 scaling 행렬을 곱해준다.
마지막으로, 해당 벡터를 다시 standart basis 인 e1, e2 로 표현되는 좌표계 공간의 값으로 표현하기 위해, 제일 처음 곱했던 공간 변환 행렬의 역행렬(이전에 변환 행렬의 역행렬은 Transpose 와 같다고 했었다)를 곱해주면, scaling 이 된 벡터를 기존 좌표계에서 잘 구할 수 있다!
오일러 변환

우리가 특정 오브젝트를 x, y, z 축을 기준으로 여러번 회전하면, 해당 오브젝트의 임의의 방향을 가리키게 된다. 이 때, 해당 오브젝트의 방향을 결정짓는 방법을 '오일러 변환(Euler transform)'이라고 부른다.
회전 각도는 '오일러 각(Euler angles)' 이라고 부르며, 이를 아래와 같이 표시한다.

위의 그림에서는 각 축에 대한 회전 변환을 한꺼번에 계산한 결과를 한 행렬로 보여주고 있다.

회전 변환은 딱히 축에 따라 순서를 지켜야 하는 것은 아니다. 즉, x, y, z 순으로 회전을 할 수도 있고, y, z, x 순으로 회전을 할 수도 있다(물론 교환 법칙은 성립하지 않는다).
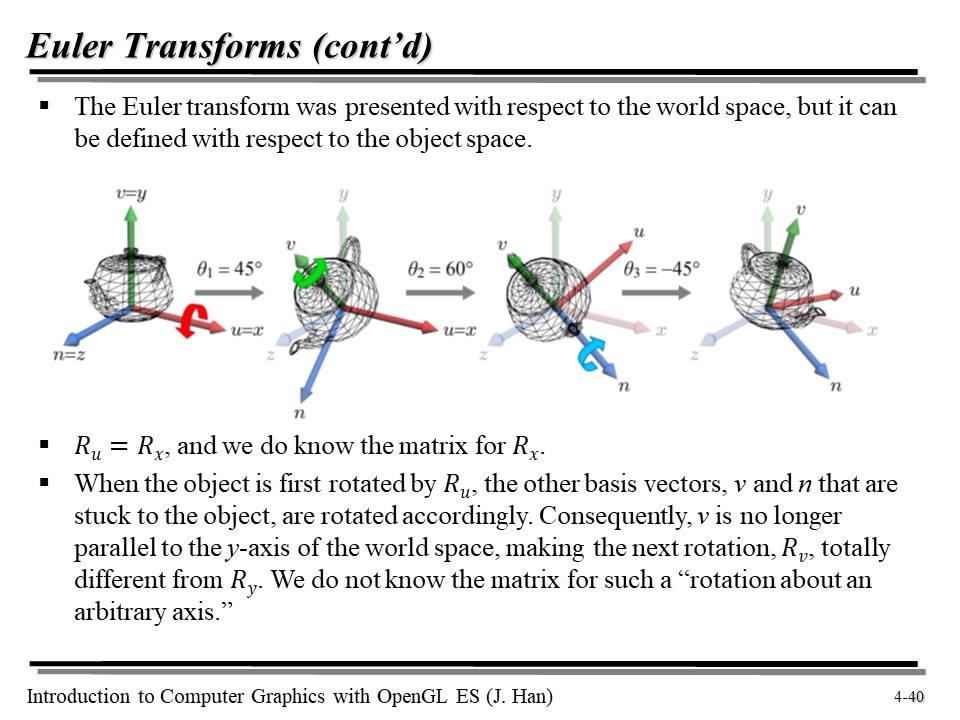
오일러 변환은 월드 공간에서 표현될 수도, 오브젝트 공간에 대해 정의될 수도 있다.
월드 공간에서의 기저 벡터를 x, y, z 로, 오브젝트 공간에서의 기저 벡터를 u, v, n 으로 정의하자.
처음에는 u = x, v = y, n = z 가 성립하지만, 오브젝트를 오브젝트 공간에서의 축에 대해 회전을 하게 되면, 월드 공간에서의 기저 벡터와 오브젝트 공간에서의 기저 벡터가 불일치하게 된다. 즉, 위 그림의 제일 오른쪽처럼, 나중에 v 에 대해 회전을 하게 되면, 월드 공간 입장에서는 해당 오브젝트가 임의의 축에 대해 회전하는 것처럼 인식된다.
그렇다면 이걸 어떻게 해결할까?

위에서, 공간 좌표계를 변환했던 방식을 응용하면 된다!
즉, 위 그림에서 틀어진 주전자를 v 축을 기준으로 회전한다고 하자. 그럼 이렇게 하면 된다 :
- v 축을 y 축에 맞게 오브젝트를 회전시킨다. 이 때의 회전 행렬을 R 이라고 하자.
- 그 다음, 회전하려고 했던 각도 (예를 들어 θ) 만큼 y 축을 기준으로 회전시킨다
- 오브젝트의 v 축을 원래의 v 축으로 되돌린다. 즉, R 의 역행렬을 곱한다.
따라서, 우리는 오브젝트 공간의 축을 기준으로 한 회전을, 월드 좌표계에서 표현할 때는 3개의 행렬의 결합이라고 이해하면 된다!
오브젝트 공간에서의 오일러 변환식은 위의 계산을 참고하자. 위에서는 주전자가 θ1 만큼, u 축을 기준으로 회전된 상태에서 다시 v 축을 기준으로 θ2 만큼 회전할 때, 행렬이 어떻게 계산되는지를 보여주고 있다.
이때, R 은 기존 u 축을 기준으로한 회전이었던 Ru(θ1) 의 역행렬이 된다.
따라서, 행렬이 소거되어 다음과 같은 식만 남게 되는 것이다.

그래서 오브젝트 공간에서의 오일러 변환은 마치 '역순으로' 회전이 이루어지는 것처럼 묘사된다.

위처럼, 회전을 한 번 더 해도 결과는 비슷하다. 위에서 행렬 Q 가 '지금까지의 회전을 다시 원상복구시키는' 역할을 한다는 것을 기억한다면, 위의 회전 변환도 아래와 같이 표현할 수 있다!

임의의 축에 대한 회전

이제 '임의의 축에 대한 회전'을 어떻게 하는지 알아보자.
주어진 축은 p1 (10, 1, 10) 과 p2 (15, 11, 10) 으로 이루어진 벡터이며, 회적 각은 60도이다. 먼저, 임의의 회전축을 기존 주축(x, y, z)에 정렬시킬 필요가 있다.
일단 p1 의 좌표를 원점에 맞춰보자. Translation 을 적용하면 될 것이다. T(-10, -1, -10) 처럼.

그리고 x, y, z 축 중 원하는 축으로 해당 축을 정렬시킨다. 위에서는 z 축에 해당 축을 맞추었다. 축을 맞추는 정렬의 과정도 회전이라는 것을 명심하자. 이때, 오브젝트 공간에서 정의된 축 u, v, n 을 월드 공간의 축 x, y, z 에 맞추는 회전 변환 행렬은 위의 R 과 같이 표현된다.

우리는 위에서 임의의 축 벡터 u, v, n 을 정의했다. 이 때 임의의 벡터 n 을 회전축으로 사용하는데... 나머지 u 와 v 는 어떻게 구해야 할까?
이때, 벡터 u 와 v 가 n 에 수직이어야 하는 것을 생각하면... u 를 다음과 같이 cross product 를 이용해 표현할 수 있다!

또한 u 는 orthonormal 해야 하기 때문에, 크기를 벡터의 길이 만큼으로 나눠주면 된다.
u 와 n 을 구했으면, v 는 n x u 로 간단하게 구할 수 있다.

3번째 단계는 z 축을 기준으로 한 회전, 4번째 단계는 2번째 단계의 역변환을 해 주면 된다. 다섯번째 단계도 첫번째 단계의 역변환이다.

결국 임의의 축에 대한 회전은 최종적으로 위와 같이 5 단계로 표현할 수 있다.
- -p1 만큼 Translation
- R 을 곱함 (오브젝트 공간의 축 벡터 u, v, n 을 월드 공간 축 벡터 x, y, z 로 변환)
- z 축을 기준으로 오브젝트를 60도 회전
- R 의 역행렬을 곱함 (월드 공간에 맞춰져 있던 오브젝트 공간의 축을 원상복귀 시킴)
- p1 만큼 Translation
위에서 1 과 5, 그리고 2 와 4 는 각각 서로가 역변환이라는 성질을 갖고 있다!




