KoreanFoodie's Study
[OpenGL ES] 4-1강 : 벡터의 회전과 변환, 아핀변환, 3차원 공간에서의 변환, 동차좌표계(Homogeneous Coordinates) 본문
[OpenGL ES] 4-1강 : 벡터의 회전과 변환, 아핀변환, 3차원 공간에서의 변환, 동차좌표계(Homogeneous Coordinates)
GoldGiver 2023. 4. 12. 00:38
이 강의는 유투브에 무료로 공개되어 있는 한정현 교수님의 컴퓨터 그래픽스 강좌를 정리한 글입니다. 자세한 내용은 강의를 직접 들으시거나 책을 구입하셔서 확인해 보세요. 강의 자료는 깃헙 링크에 올라와 있습니다.
요약 :
1. 아핀변환은 Scaling, Rotation, Translation 행렬의 결합으로, [L|t] 로 표현할 수 있다. 아무리 많은 변환을 해도 결국 단일한 [L|t] 로 표현 가능하다!
2. 행렬에서 열을 하나 추가해 확장을 시키면, Translation 을 행렬을 이용해 표현할 수 있는데, 이렇듯 확장된 행렬의 좌표계를 동차좌표계(Homogeneous Coordinates) 라고 한다.
3. 원점이 아닌 점을 기준으로 물체를 회전하려면, 기준 점을 원점으로 Translation 후, 회전을 적용하고 Translation 을 하여 기준점 위치를 복구시켜 주면 된다!
Scaling 과 Rotation
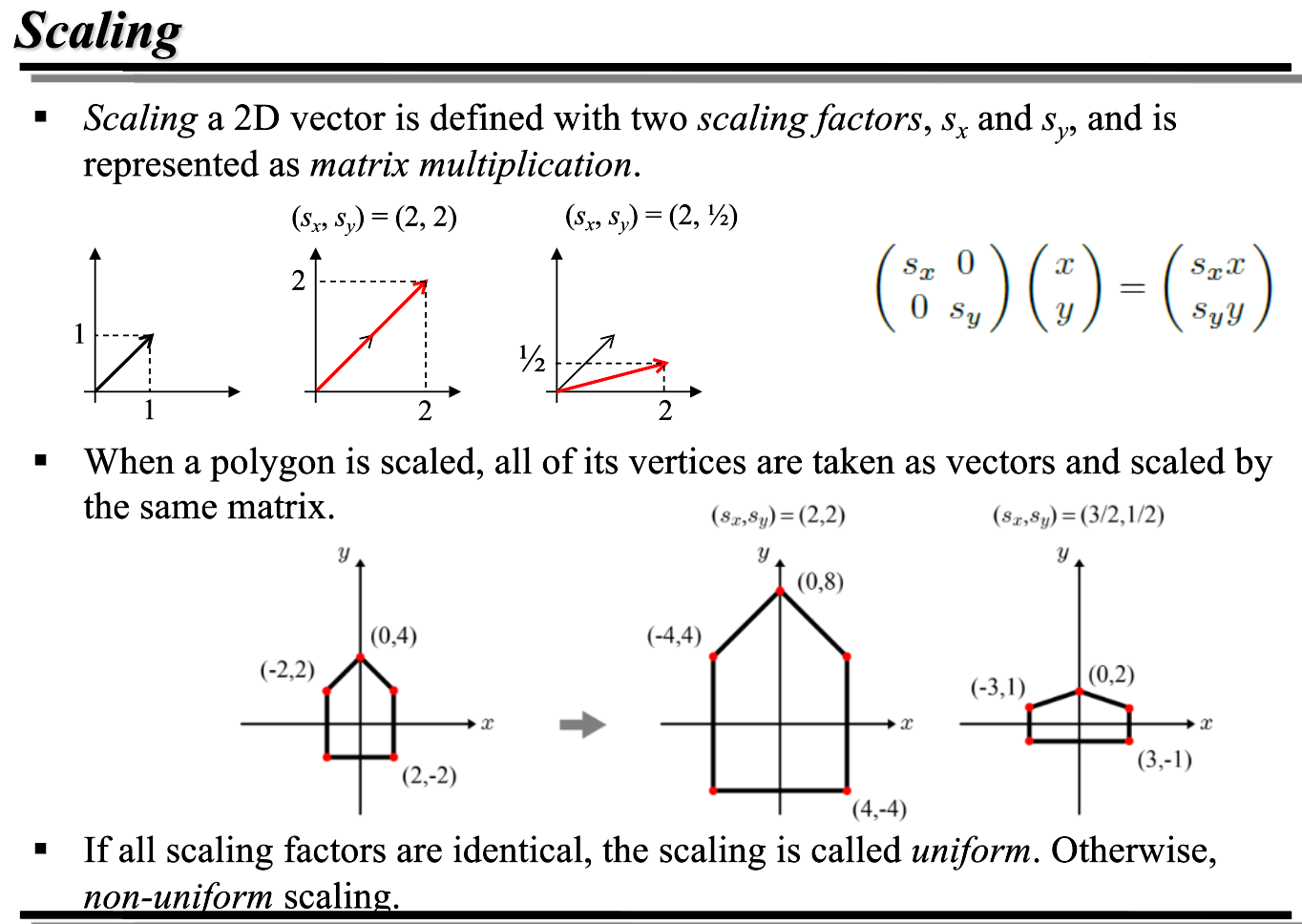
2D 벡터를 스케일링하려면 sx sy 라는 scaling factor 가 필요하다. 그리고 위에 보이는 것처럼, 행렬 연산을 통해 간단히 이루어진다. 만약 모든 scaling factor 가 동일하면, 해당 스케일링은 uniform 하다고 한다(그렇지 않으면 non-uniform)

그럼 이제 한 번 회전을 보자. 벡터의 회전은 위와 같은 행렬식을 통해 이루어진다.

기본적으로 회전은 반시계 방향을 기준으로 이루어진다. 시계 방향으로의 회전은 회전하려는 각도에 '-' 를 붙이면 된다.
Translation and Homogeneous Coordinates

Scaling 과 Rotation 과 달리, translation 은 벡터 addition 으로 표현된다. 위의 행렬식 (x, y) 에 (dx, dy) 를 더하는 것처럼 말이다.
하지만 다행히도, homogeneous coordinates(동차좌표계)를 사용하면, translation 을 matrix multiplication(행렬곱) 으로 표현할 수 있다.
그 비법은 행과 열을 하나 추가한 다음, 맨 마지막 열에 translation 을 할 factor 를 넣고 행렬 곱을 하는 것이다!

위에서는 2D 벡터의 동차좌표계를 만들 때 마지막 요소에 1을 넣었지만, 사실 반드시 1 을 넣어야 하는 것은 아니다. 임의의 미지수 w 가 들어갈 수 있다.
만약 추가되는 요소의 값이 1이 아닐 경우, 해당 벡터 (X, Y, w) 를 w 로 나누면 (X/w, Y/w, 1) 을 갖게 되는데, 이때의 (X/w, Y/w) 는 Cartesian coordinates 를 의미하게 된다.
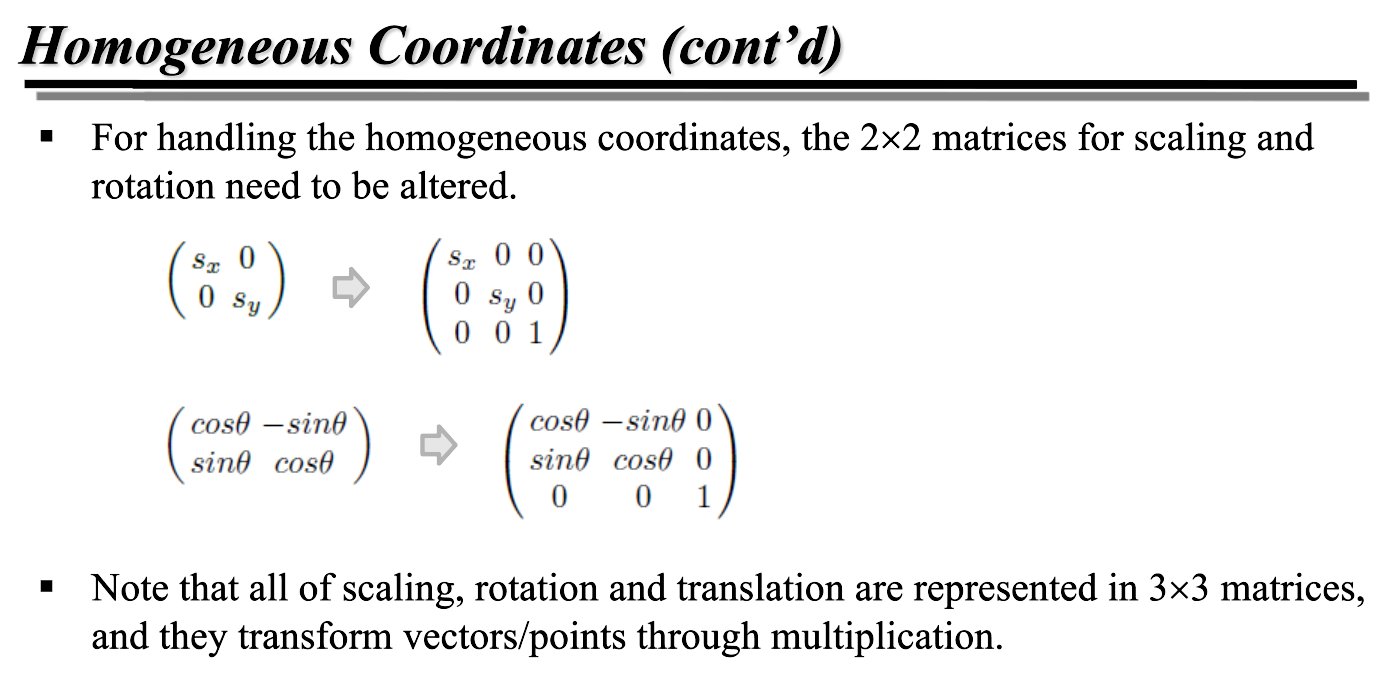
2D 벡터의 동차좌표계를 다룰 때는, 기존에 scaling 과 rotation 에 사용했던 2x2 행렬은 위와 같이 확장되어야 한다.
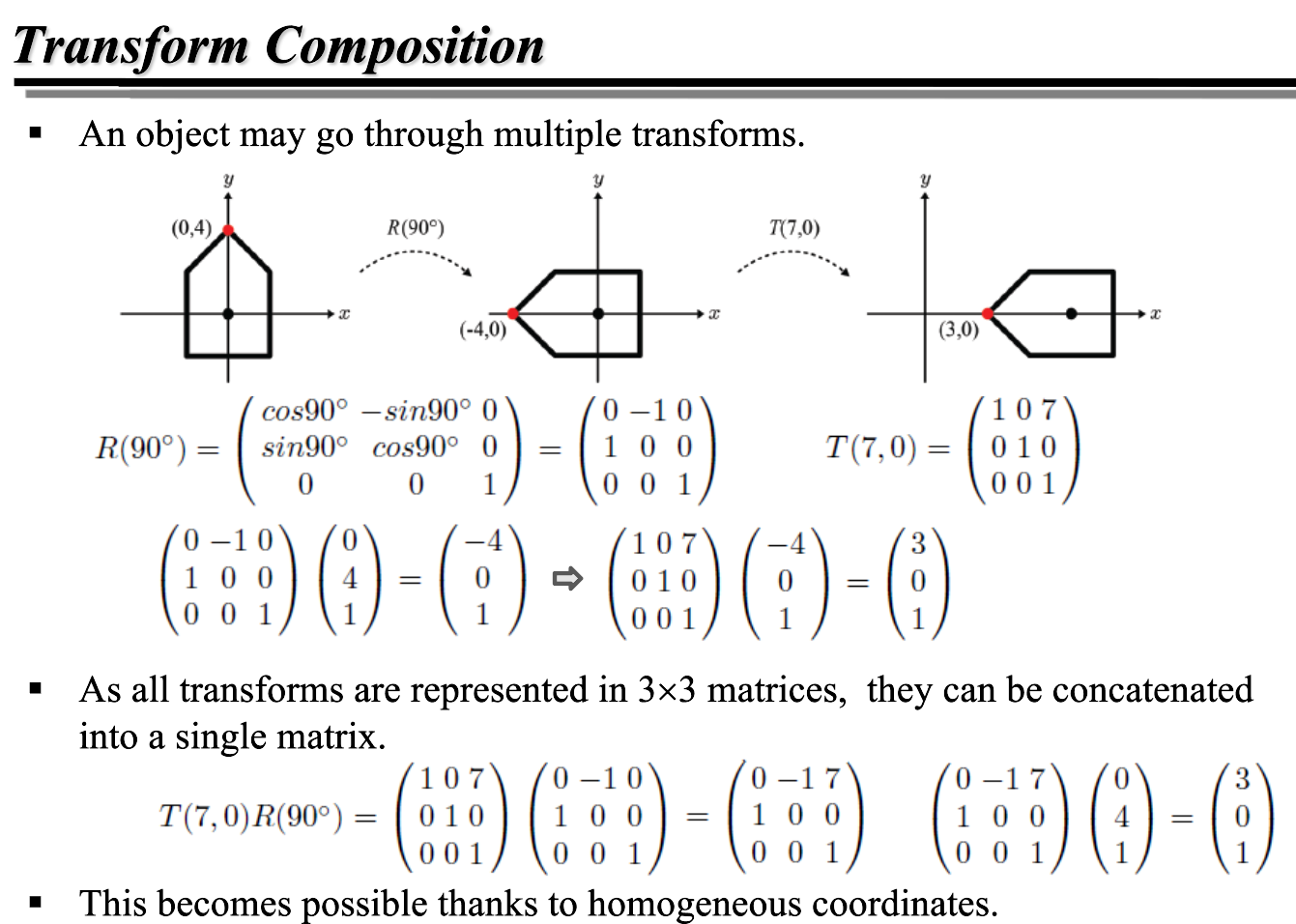
위와 같이 여러 변환을 거치는 오브젝트가 있다고 하자. Rotation 과 Translation 이 동시에 있는 이 변환은, 동차좌표계를 사용하면 변환을 하나의 행렬로 압축할 수 있다. 결국 행렬곱으로 표현될 것이기 때문이다!

단, 행렬곱은 교환법칙이 성립하지 않는다. 따라서, 회전 후 Translation 을 하는 것과 translation 을 한 후 회전을 한 결과는 다르게 나온다!

우리는 지금껏 원점에 대한 rotation 과 scaling 을 다루었다. 그런데 만약 원점이 아닌 임의의 점 (a, b)을 기준으로 한 회전은 어떻게 적용해야 할까?
답은 간단하다. 먼저 회전하려는 점 (x, y) 를 (-a, -b) 만큼 translation 한다. 그 후, 회전을 적용한 다음, 다시 (a, b) 만큼 translation 을 해 주면 된다!
아핀 변환

아핀 변환은 선형 변환에 이동이 결합된 것이다. 얼마나 많은 아핀 변환이 적용되었든 간에, 그러한 변환들은 결국 행렬로 합쳐질 수 있다. 그리고 3번째 행은 언제나 (0 0 1) 이 될 것이다(2D 벡터의 변환의 경우).

아핀 행렬의 세 번째 행을 잠시 무시하면, 우리는 나머지 2 x 3 행렬을 [L|t] 로 표현할 수 있다. 이때, L 을 2 x 2 행렬로, t 를 2D 열 벡터로 생각하자.
이때 L 은 '결합된' 선형 변환들을 의미한다. 이는 translation 이 포함되지 않은 녀석이라는 뜻이다.
반면 t 는 '결합된' 이동 변환들을 의미한다. 즉 translation 만 합쳐진 녀석이라는 뜻이다.
실제로 위 그림을 보면, TR 과 RT 에서의 L 은 동일한 값을 갖고 있는 것을 확인할 수 있다!

위 그림은 회전 각도가 90 도인 경우, RT 와 R 의 L 이 같다는 것을 보여준다. 다만 t 는 그 값이 달라졌다.

아핀변환([L|t]) 에서, L 은 t 보다 먼저 적용된다. 얼마나 많은 아핀 변환을 하든, 우리는 [L|t] 로 표현되는 행렬 하나를 얻어낼 수 있다.
만약 특정 점 p 를 아핀변환한다고 하면, 우리는 이를 Lp + t 로 표현할 수 있다!

위 식은 아핀 변환을 적용할 때, 회전을 이동 변환보다 이전에 적용하는 예시를 보여준다.

scaling 이 개입하지 않고 rotation 과 translation 만으로 변환이 이루어지는 경우, 변환되는 오브젝트의 형태는 변함이 없을 것이다. 이런 변환을 강체 변환(Rigid Motion)이라고 한다.
얼마나 많은 아핀 변환이 적용되었든지 간에, 우리는 이를 결합한 하나의 행렬 [R|t] 로 표현할 수 있다.
위의 [R|t] 도 물론 R 이 t 보다 먼저 적용될 것이다.
3D 에서의 변환
이전에는 2D 벡터를 다루었으니, 간단히 3D 공간의 오브젝트들이 어떻게 변환되는지를 간단하게만 살펴보자.
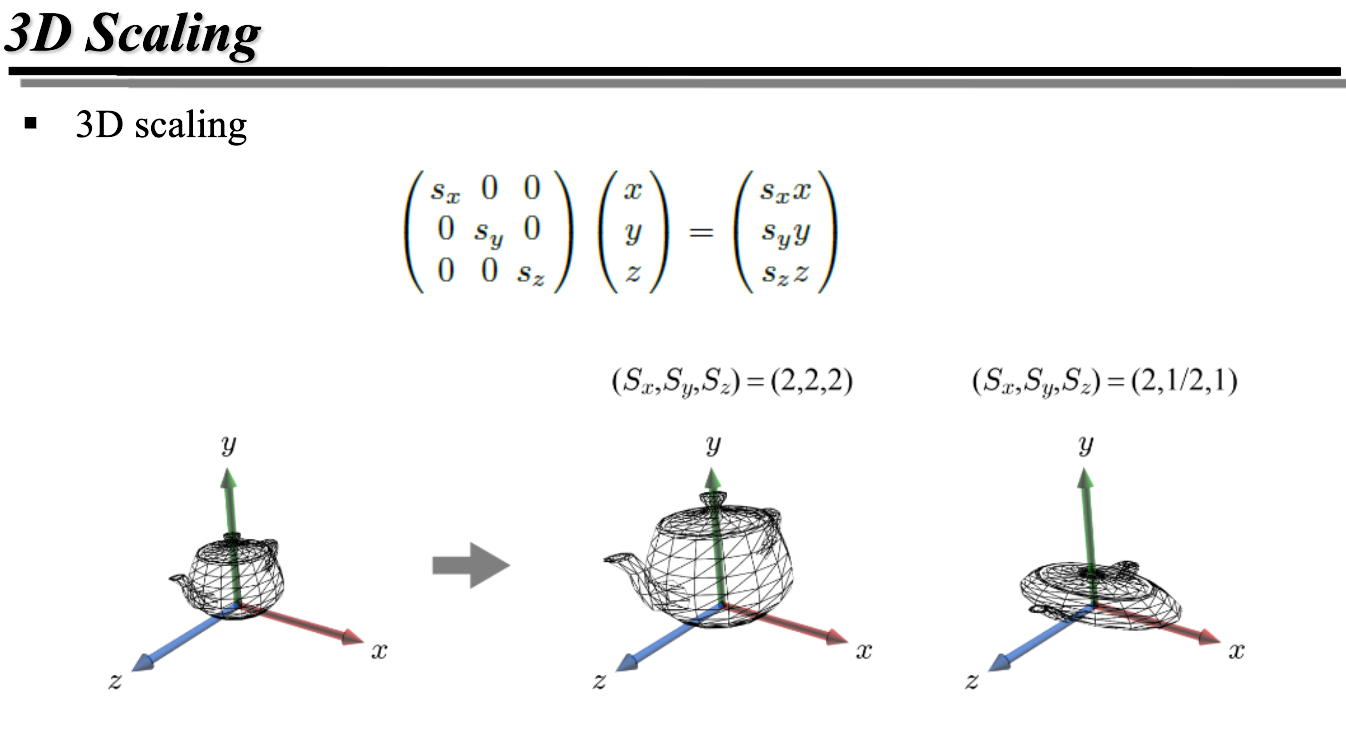
3D 영역에서의 스케일 예시이다. 주전자를 찌그러뜨리고 있다. 2D 의 경우와 별반 다를 것은 없다.

다만 3D 영역의 회전은, 2D 와 달리 회전 축(axis of rotation) 을 필요로 한다. 위의 예시는 z 축을 기준으로 한 회전을 보여준다. p 가 p' 로 바뀌고 있다.

그럼 Rx, 즉 x 축을 기준으로 한 회전은 어떨까?
간단하다! 오른손 법칙을 떠올려 보면, z 축을 기준으로 했을때 우리는 x 축에서 시작해 y 축으로 감싸 쥐었다. 그럼 x 축을 기준으로 하면... y 축을 기준으로, z 축 방향으로 손바닥을 감싸쥐게 된다.
즉, x' 를 y' 로, y' 를 z' 로 바꿔 생각하면, 위와 같이 x 축을 기준으로 하는 회전 변환 행렬을 간단하게 구할 수 있다!

2D 에서의 회전에서, 반시계 방향의 회전이 양의 각도만큼의 회전을 의미했었다. 그렇다면 3D 에서는 어떨까?
3D 회전에서 축이 당신의 눈을 향한다고 생각해보자.
- 회전이 반시계 방향이라면 : 회전 각도는 양수이다
- 회전이 시계 방향이라면 : 회전 각도는 음수이며, 행렬도 이에 맞게 정의된다
좋은 방법은 : 먼저 회전 축을 엄지와 정렬시킨 다음, 만약 손바닥을 그러쥐는 방향이 회전을 하려는 방향과 일치한다면, 회전각도는 양수라고 정하는 것이다(반대면 음수). -𝛉 만큼의 회전은 2π - 𝛉 만큼의 회전과 같다는 것을 기억해 두자.
'Game Dev > OpenGL ES' 카테고리의 다른 글
| [OpenGL ES] 5강 : 렌더링 파이프라인, 카메라 공간, 뷰 변환(View Transform), 오른손 좌표계와 왼손 좌표계, 절두체 (0) | 2023.04.14 |
|---|---|
| [OpenGL ES] 4-2강 : 월드 공간, 오브젝트 공간, 오일러 변환, 임의의 축에 대한 회전 (0) | 2023.04.12 |
| [OpenGL ES] 3강 : 모델링, 폴리곤 메시, 표면 법선(Surface Normal), 정점 법선(Vertex Normal) (0) | 2023.04.11 |
| [OpenGL ES] 2강 : 벡터의 내적/외적, 선형 보간(Linear Interpolation) (0) | 2023.04.11 |
| [OpenGL ES] 1강 : 그래픽스 개론, 모델링, 리깅, 애니메이션, 렌더링 (0) | 2023.04.11 |




