[OpenGL ES] 16강 : 전역 조명, 레이 트레이싱, 그림자 광선, 반사광, 굴절광, 라이트 매핑, 환경 매핑, 큐브 매핑

이 강의는 유투브에 무료로 공개되어 있는 한정현 교수님의 컴퓨터 그래픽스 강좌를 정리한 글입니다. 자세한 내용은 강의를 직접 들으시거나 책을 구입하셔서 확인해 보세요. 강의 자료는 깃헙 링크에 올라와 있습니다.

---

요약 :

1. Phong 라이팅 모델은 local illumination 을 만들어내는 데는 유용하지만, 전역 조명(Global Illumination) 을 자연스럽게 만들어내기 위해서는, 3 가지 추가적인 요소를 고려해야 한다. 즉, 그림자 광선(Shadow Ray), 반사광(Reflection Ray), 굴절광(Transmitted/Refraction Ray) 을 반영해야 한다.

2. 레이 트레이싱 기법은 재귀적으로 Ray 값들을 계산하여 색상을 계산한다. 각 Ray 는 Primary Ray 가 되어 위에서 설명한 shadow/Reflection/Refraction Ray 를 만들어 내는데, 각 Ray 는 정해진 반사 계수만큼 Tree 처럼 가지치기를 계속해 나갈 것이다.

3. 주변 환경을 담아내는 텍스처를 만드는 기법으로 환경 매핑(Environment Mapping)이 있고, 이 경우 큐브 매핑(Cube Mapping)을 이용한다. 즉, 텍스처를 정육각형으로 감싼 후, 반사되는 것을 각 면에 기록하는 방식으로, Ray Tracing 을 1 번만 한 결과라고 이해하면 쉽다. 다만 오목한 면의 경우 큐브 매핑이 잘 작동하지 않는다. 

전역 조명과 텍스처링

Lighting 과 Illumination 은 두 가지로 나눌 수 있다. 바로 Local 과 Global 이다.
Phong 모델은 local illumination 을 표현하는 모델인데, 현실에서는 (a) 나 (b) 와 달리 (c) 처럼 반사광에 의해 물체가 빛나게 된다. 🤨
 
 

레이 트레이싱(Ray Tracing)

Ray tracing 은 global illumination 을 구현하기 위해 만들어진 알고리즘 중에 거의 처음으로 제안된 녀석이다.
절두체에서, 해상도만큼 (즉, 픽셀의 갯수만큼) Ray 를 쐈다고 가정해 보자. 이런 Ray 를 Primary Ray 라고 한다. 이런 Primary Ray 는 세 개의 부차적인 Ray 를 생성하는데...
 

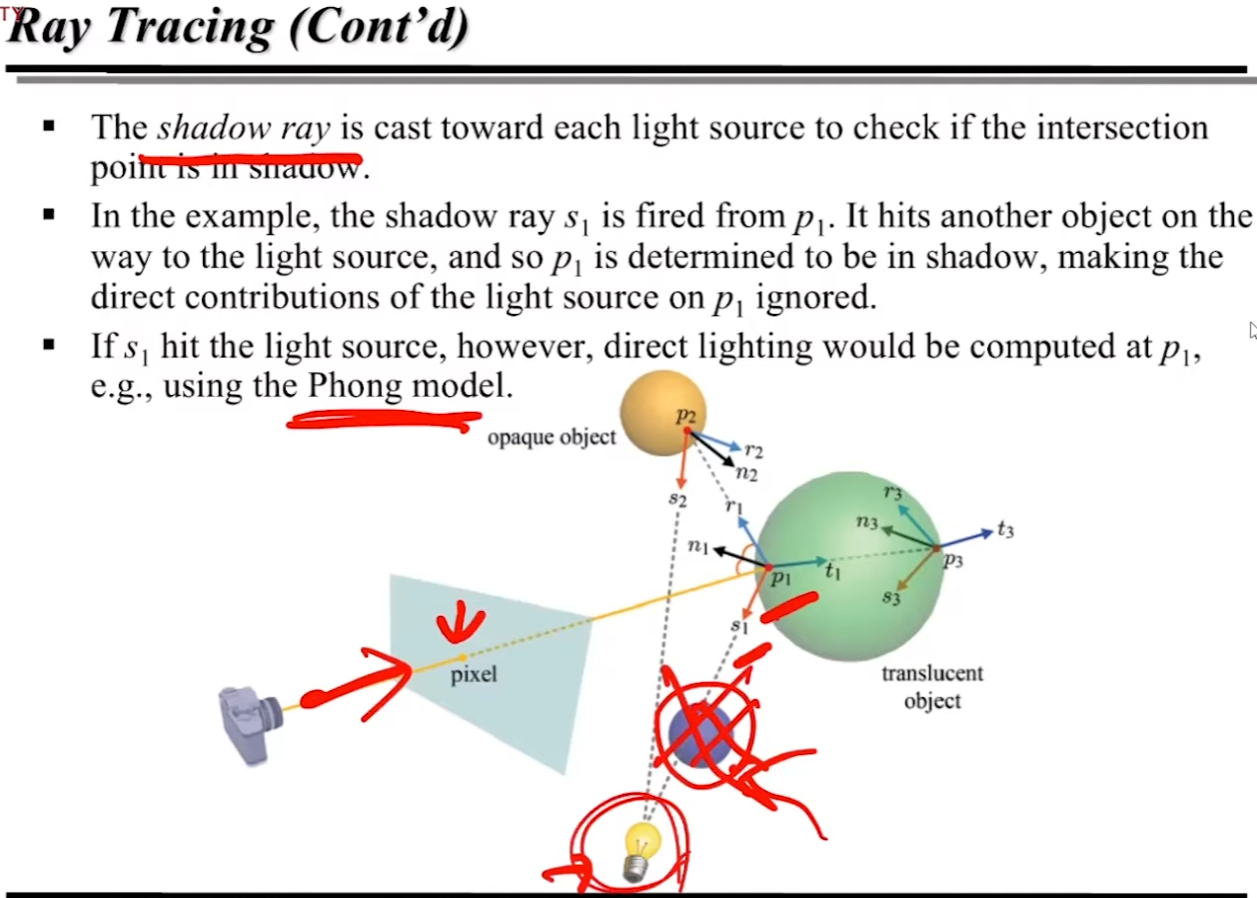
일단 Shadow Ray 부터 보자.
일단 카메라로부터, Ray 를 쏜다고 했을 때, 해당 Ray 가 초록색 공에 부딪혔다고 가정하자. 이때의 점은 p1 이 되는데... p1 의 경우, light source 로부터 직접적으로 빛을 받지 못하고 있다. 즉, p1 점의 경우, 그림자가 질 것이라고 간주될 것이다. s1 은 shadow ray 로, 그림자가 질 경우에는 s1 과 부딪히는 녀석은 빛을 받지 못하는 것으로 인식될 것이다. 반면 p2 처럼 빛을 실제로 받는 녀석은, s2 와 부딪힌 녀석은 Phong 모델을 적용하여 Lighting 을 처리하면 된다! 😄
 

그 다음은 Reflection Ray 이다.
Reflection Ray 는, 말 그대로 반사광이다. I1 을 입사광이라고 생각하고, n1 을 normal vector 라고 보면, 입사각 = 반사각이 되는 벡터 r1 을 그릴 수 있다.
해당 r1 의 계산은, 이전의 Phong 모델에서 Reflection Ray 를 계산할 때의 식을 그대로 사용하면 된다. 다만 한 가지 주의할 점은... Phong 모델에서는 i 가 점으로부터 뻗어나왔는데, 여기는 들어오고 있어서, 방향이 반대이다. 즉, i 대신 -i 를 곱해주면 적절한 r 을 구할 수 있다!
 

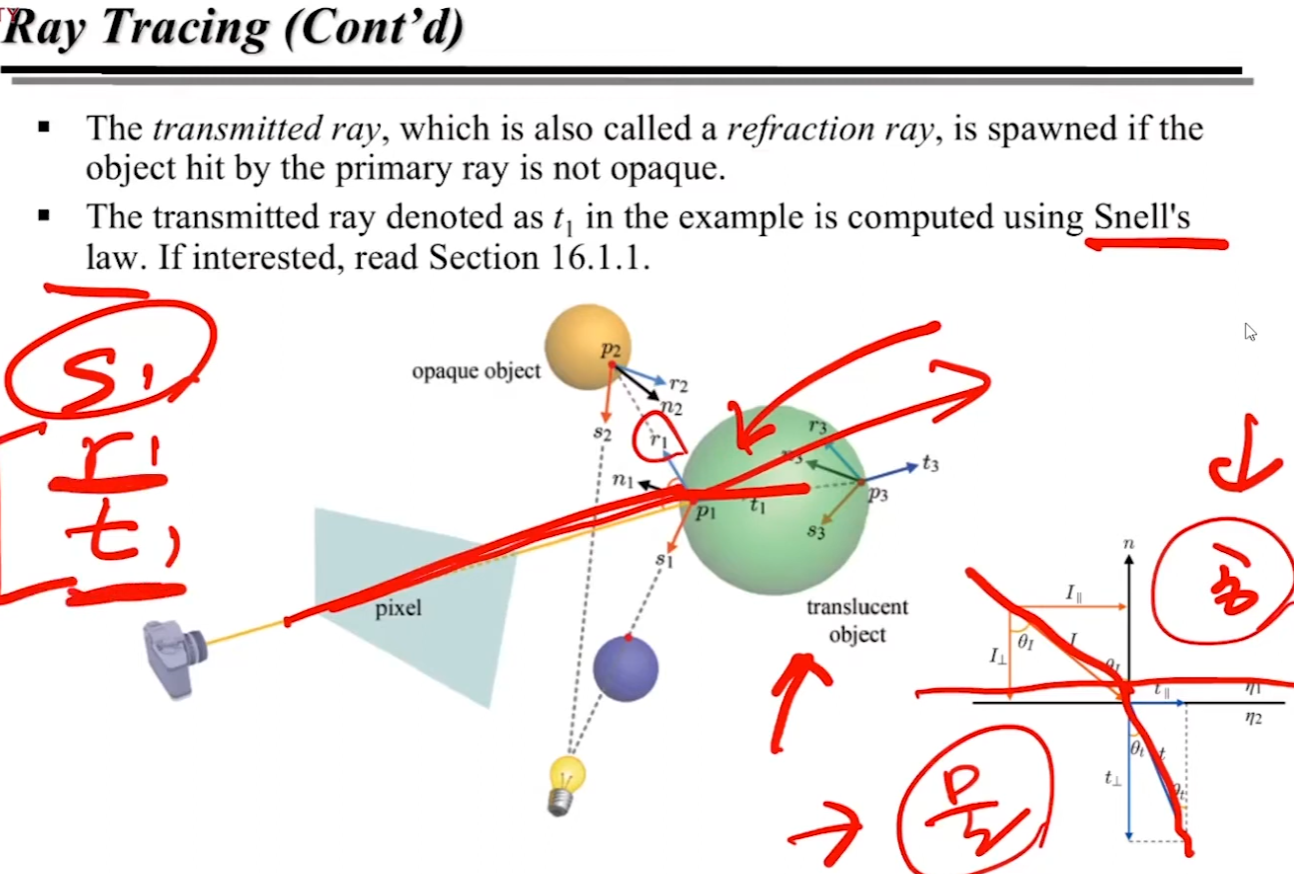
이제 마지막으로 Refraction Ray 를 보자. 한글로는 굴절광인데, 완전히 불투명하지 않은 오브젝트 (즉, 물처럼 반투명한) 와 부딪혔을 때 굴절광이 만들어진다.
정확한 계산을 위해선 Snell's Law 를 활용해야 하므로, 따로 찾아보도록 하자 😅
 

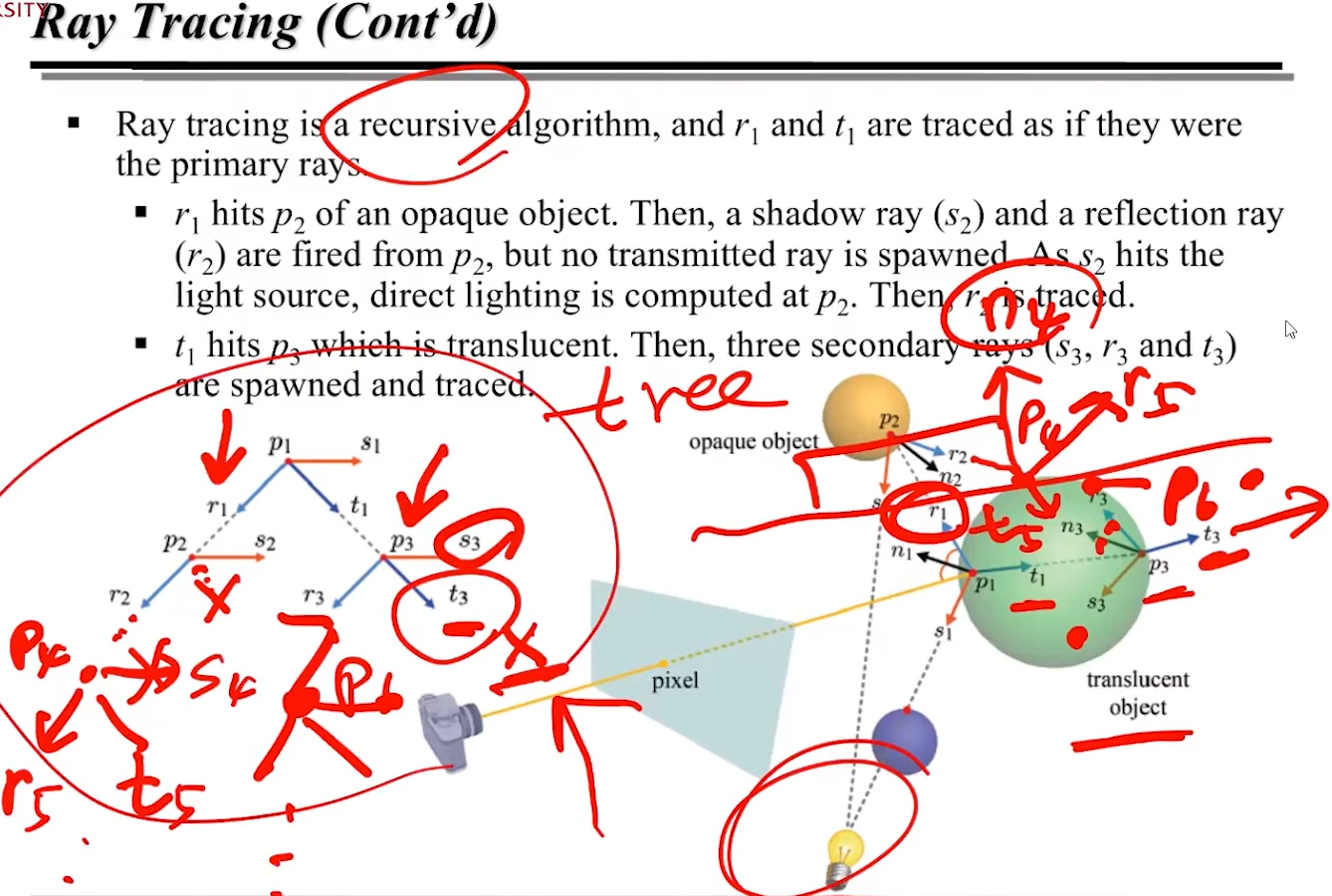
그런데 Ray Tracing 은 Recursive 한 알고리즘이다. 즉, r1 과 t1 은 다른 녀석들의 Primary Ray 처럼 작동한다.
즉, 왼쪽 그림의 Tree 형태로 Propagate 될 것이다! 😉
Recursive 알고리즘이라면 탈출조건은 어떻게 될까? 부딪힌 점의 각도가 90도보다 크면, 더 이상 재귀가 일어나지 않을 것이다 😄
 

ray tree 는 ray 가 물체와 더 이상 부딪히지 않거나 미리 정해진 횟수 이상 반사가 되면 더 이상 확장되지 않는다.
reflection ray 를 통해 계산된 색상은 표면의 specular reflectance 계수 (Ms) 와 곱해지고, transmitted ray(굴절광) 을 통해 계산된 색상은 material specific transmission 계수와 곱해진다.
위에서 계산된 색상값들은 shadow ray 를 통해 계산된 색상과 더해지게 된다!
 

위 그림은 Ray Tracing 을 사용해 만든 이미지이다 😄
Ray Tracing 은 매우 고급진 녀석이지만, 실시간으로 연산하는 데 시간이 많이 걸리므로 주로 영화 같은 비실시간 그래픽 처리에서 많이 사용한다 😅

 

 

라이트 매핑(Light Mapping)

오브젝트와 Light Source 가 정적이라고 할 때, diffuse reflection 은 카메라 위치에 관계없이 일정하다.

퐁 모델에서 diffuse reflection 을 생각해 보자. 미리 계산한 

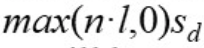
이 값은, irradiance 를 의미하며, 들어오는 빛의 양을 말한다. 또한 md 의 경우, 런타임에 읽은 image texture 의 값이다.

즉, irradiance 는 미리 계산이 가능하며, 이것은 light map 이라는 이름으로 저장된다.

여기서 "도대체 irradiance 가 무엇이지" 라는 의문이 생길텐데... 그걸 알려면 래디오시티(Radiosity) 알고리즘(위키피디아는 라디오서티 라고 번역해놨다;) 를 이해해햐 한다. Radiosity 는, 각 점과 점 사이의 (혹은 메시 조각과 메시 조각 사이) 빛의 반사 정도를 측정한 값이라고 봐도 무방하다.

 

책 16강을 보면 명확히 이해가 가도록 나왔는데... 요약하여 설명해 보도록 하겠다. 이미지는 위키피디아와 엔비디아에서 갖고 왔다.

일단, 표면 i 와 j 가 있다고 하자. 이때, 우리는 i 에서 반사된 빛이 j 로 들어갈 때, 얼마나 들어갈지를 계산할 것이다(j -> i 의 경우도 계산할 것임).

이때, i, j 의 표면처럼 메시를 잘게 쪼갠 것은 패치(Patch) 라고 하고, 이때의 각 패치가 다른 패치에게 보이는 정도(혹은 빛을 반사하는 정도)를 폼 팩터(Form Factor) 라고 한다. 우리는 각 패치 사이의 폼 팩터를 계산하여, 빛이 반사되는 정도를 파악할 것이다.

아... 근데 이걸 책보다 더 잘 설명할 자신이 없다; 그래서 그냥 책 내용을 캡쳐해서 올릴테니, 참고하도록 하자 ㅠ...

그냥 책을 사라는 뜻이다! 😅

 

 

irradiance 는 미리 계산되는 녀석이다보니, 실시간에서도 전역 조명을 적용할 수 있다(어차피 라이트 맵 계산은 런타임에서 안하니까). 라이트 맵을 만드는 방식은 14강에서 노멀 맵을 만드는 방식과 유사하다! 😄
 
 

 

환경 매핑(Environment Mapping) 과 큐브 매핑(Cube Mapping)

위처럼 주변을 반사하는 오브젝트는 어떻게 렌더링할 수 있을까? 이런 녀석들을 environment map 이라고도 부른다.
cube map 을 이용해 environment map 을 만드는 기법을 소개한다.
 

개념적으로, cube map 이 오브젝트를 감싼다고 하자. viewpoint 로부터 발사된 ray 를 p 에 비친 색상을 결정하는데 사용해 보자.
이건... 사실 Ray Tracing 을 하되, 반사 계수를 1로 설정한 것과 동일하다 😉 반사된 녀석의 값을 그대로 cube map 에 기록하면 되기 때문이다! 하지만, 아쉽게도 concave(오목한) 오브젝트는 처리할 수 없다. 왜냐하면 오목한 녀석은 빛을 반사하지 않을 것이기 때문이다!
 

실제 OpenGL 에서는 Cube Map 에 필요한 변수들이 이미 선언되어 있다 😃
 

Cube Mapping 을 만드는 방법은, 이전에서 텍스쳐 맵을 만드는 것과 유사하다. Generate 하고, Binding 한 후, 값을 채워주기만 하면 된다!
 

Vertex Shader 를 보자. Cube Mapping 을 적용할 경우, 이제 Vertex Shader 에서 텍스쳐를 위한 연산을 미리해줄 필요도 사라진다 😆
 

이제 Cube Mapping 만 해주는 Fragment Shader 를 보자.
이 녀석은 Normal, View, Reflection 을 계산하는데... Reflection 을 계산할 때, i 벡터와 View 벡터는 방향이 반대니까, i 에 -view 만 넣어주면 계산이 끝난다!
 

그런데 NVIDIA 의 경우, 레이 트레이싱을 지원하는 RTX 그래픽 카드를 내놓았다. AMD 는 Radeon 을 선보였고...
그래서, 실제로 게임에서도 이제 Ray Tracing 을 하고 있는 시대가 열렸다. 😮
 
 

Ambient Occulusion

이제 Ambient Occulusion 에 대해 알아보자.
Phong 모델에서 ambient term 을 고려해 보면, 간접광으로 인해 빛을 받는 부분을 계산할 때 실제로는 오목한 부분에서 빛을 잘 받지 못하는 부분이 존재한다는 것을 알 수 있다. 이 경우, 몇몇의 방향들은 occulud 되는데, 이때 반구를 기준으로, 뻗어나가지 못하는 양을 나눈 값을 occulusion degree 라고 부른다.
 

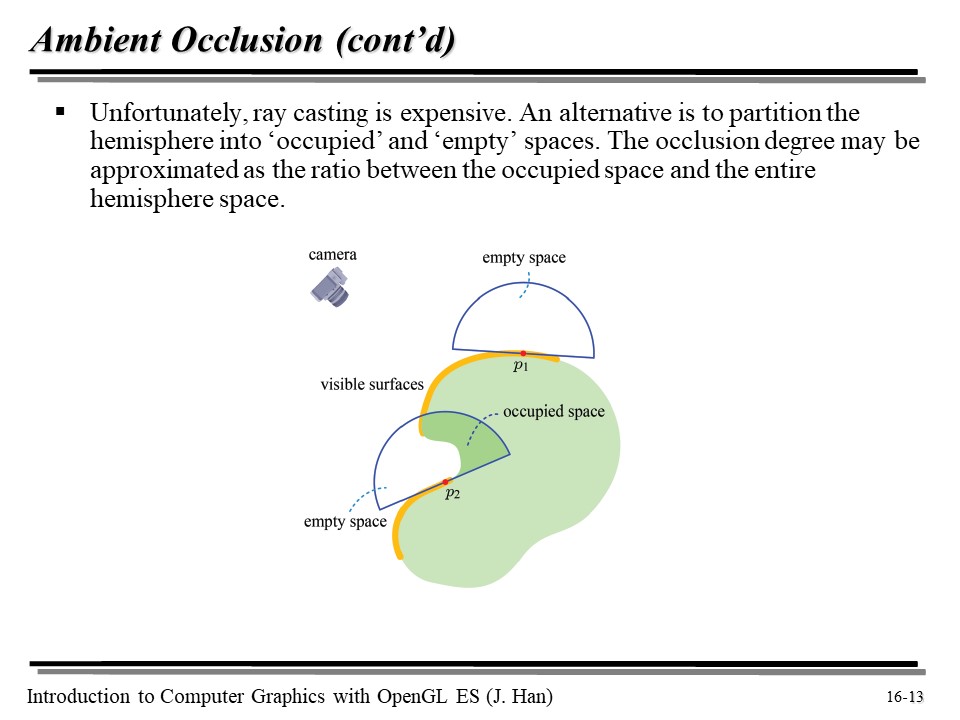
그런데 Ray Casting 은 비싸다... 그래서, 대안으로 반구를 그린 다음, 겹친 영역을 계산하여 degree 를 만들어낼 수도 있다!
 

그 후, 반구 내의 샘플 포인트를 잡아 다시 보간을 진행한다.
카메라로부터... shadow map 을 만드는 것처럼, depth 값을 계산하여 Occulusion Degree 를 만들 수 있다!
 

이는 Ambient Occulusion 을 감안한 결과물이다 😊
 

그런데 Ambient Occulusion 으로도 위와 같은 오브젝트는 자연스럽게 렌더링하기 어렵다. 하지만 이런 케이스는 극소수이므로, Ambient Occulusion 은 여전히 게임에서 널리 사용되고 있다 😄