[OpenGL ES] 14강 : 노말 매핑(Normal Mapping), Height Map, 탄젠트 공간(Tangent Space), Tangent-Space Normal Mapping

이 강의는 유투브에 무료로 공개되어 있는 한정현 교수님의 컴퓨터 그래픽스 강좌를 정리한 글입니다. 자세한 내용은 강의를 직접 들으시거나 책을 구입하셔서 확인해 보세요. 강의 자료는 깃헙 링크에 올라와 있습니다.

---

요약 :

1. 고해상도 메시에서, 실시간으로 라이팅을 처리하는데는 비용이 많이 들 것이다. 이를 해결하기 위해, 노말 매핑(Normal Mapping) 과 저해상도 메시를 사용하여 효율적으로 그럴듯한 라이팅 효과를 만들어낼 수 있다.

2. 노말 맵을 만드는 대중적인 방법으로는 Height Field 가 있다. 메시에서 한 점에 인접한 4개의 점에서 각 2개의 점씩 직선의 방정식을 만든 다음, 두 직선 벡터에 대해 외적을 취하는 방법이다. 그럼 (x, y) 좌표에 대한 z 의 값을 방정식으로 표현할 수 있고, 해당 방정식이 노말 벡터를 의미할 것이다!

3. 탄젠트 공간(Tangent Space) 는 표면 위의 한 점을 원점으로 하는 좌표계를 의미한다. 이때의 Basis 인 T, B, N 은 각각 표면의 접선 벡터 2쌍과 노말 벡터 (0, 0, 1) 을 의미한다. 라이팅을 처리하기 위해서는 World Space 에 있는 Light 벡터와 Tangent Space 에 있는 노말 벡터의 내적을 취해야 하는데... 탄젠트 공간의 Basis 를 통해 Light 벡터를 탄젠트 공간으로 변환할 수 있다!

Bumpy Surfaces

위의 그림처럼 고주파 Polygon Mesh 를 렌더링한다고 생각해보자. 그런데, 이런 고주파 메시를 렌더링하는 비용은 상당히 크다. 왜냐하면, (d) 의 그림처럼 각 오르막과 내리막에서 Lighting 처리를 해 주어야 하기 때문이다!

 

반면, (a) 그림처럼 저해상도 메시르 렌더링한다로 생각하면, 비용은 작지만 저품질의 그래픽을 얻게 된다.

 

 

노멀 매핑(Normal Mapping)

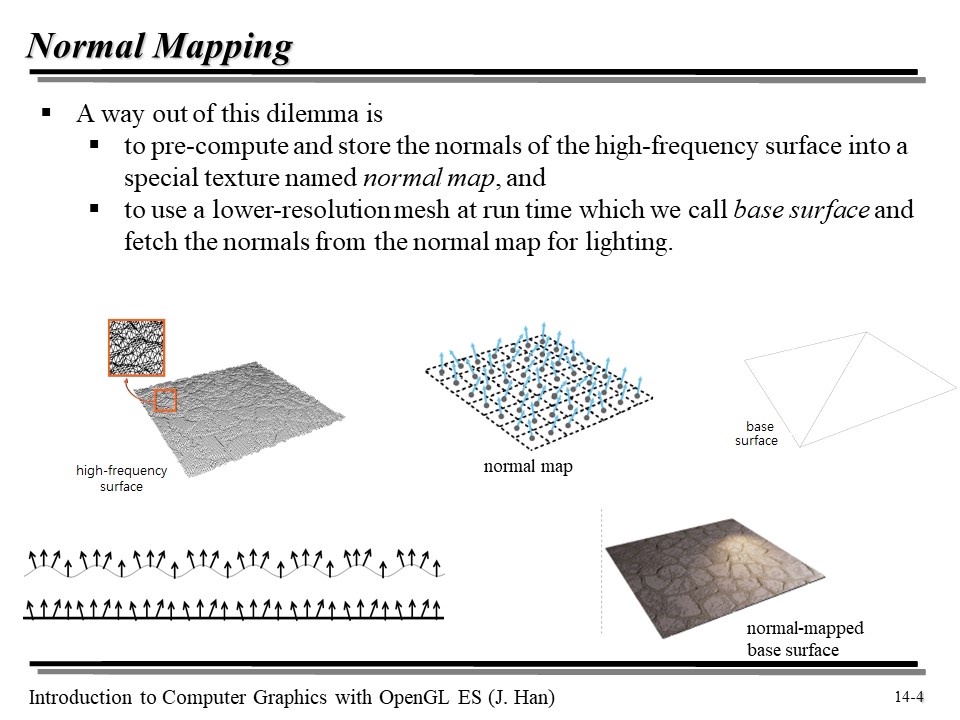
이런 딜레마를 해결하기 위해, normal map 이라는 특별한 텍스쳐를 이용하여 고주파 표면의 노멀을 미리 저장해 놓는다.

그리고 저해상도의 메시를 런타임에 base surface 로 사용하고, 라이팅을 할 때는 미리 계산해 놓은 normal map 을 사용하면, 이 딜레마를 어느 정도 해결할 수 있다!

 

 

Height Field

대중적인 방식으로 Height Field 가 있다. 이 방식은 주어진 x, y 좌표에 대해 h(x, y) 함수를 만들고, 해당 값들을 height map 이라는 텍스쳐에 저장한다.

height map 에 저장된 값들은 gray scale 값으로 표현할 수도 있다. 왜냐하면 각 값들이 0 에서 255 사이에 있도록 조정할 수 있기 때문이다!

 

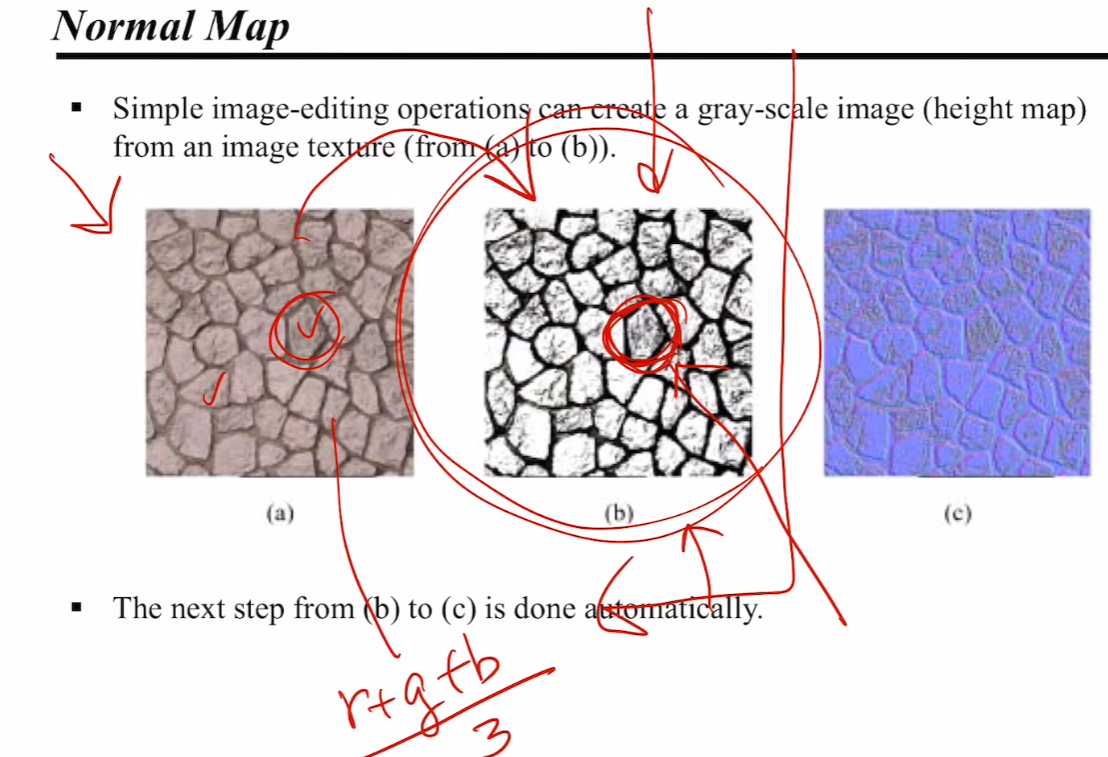
그런데 사실 간단한 계산만으로 이미지 파일에서 그레이 스케일 이미지를 뽑아낼 수 있다. 그냥 R, G, B 값을 다 더한 후, 3으로 나눈 값을 넣어주면 되니까!

그렇게 해서 나온 결과가 (a) -> (b) 이다.  (b) -> (c) 의 단계는 자동으로 진행된다. 그건 다음 슬라이드에서 설명할 것이다 😅

 

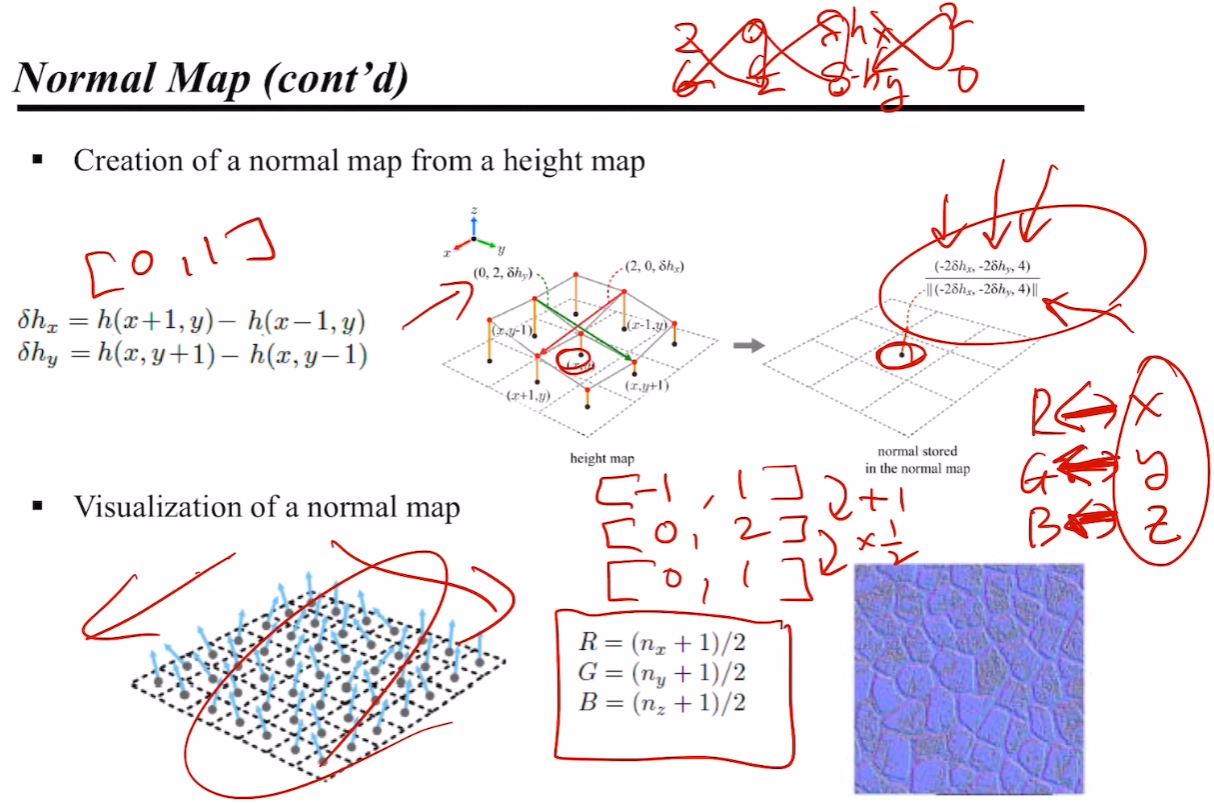
위 그림을 보면.. 한 height 점에서 교차하는 두 개의 직선을 구할 수 있다. 인접한 점 4개가 나오고, 2개씩 이으면 되니까. 이때, 이은 선분에서의 변화량을  δhx, δhy 이라고 정의하면... 우리는 노말을 두 직선의 cross product 를 취함으로써 쉽게 구할 수 있다! 뭐.. Normalize 는 뒤에 해 주면 된다.

그렇게 해서 나온 결과값을 그리면, 오른쪽 아래처럼 파랗게 나오게 되는데... 왜 파랗게 나올까?

왜냐하면 이게 '노말 맵'이기 때문이다! 😄 수수께끼가 아니라... 위처럼 절벽같은 곳이 아니라면, 일반적으로 z 축의 값이 더 클것임이 자명하다 😉

 

마지막으로... 만약 노말 매핑을 촘촘하게 구하고 싶은데, 메시는 저주파일 경우는 어떻게 할까? 예를 들어, 한 폴리곤 메시 의 가로 세로 크기가 100 이라고 하자.

그럴 경우, 우리가 Ray Intersection 에서 했던 원리를 응용하면 된다. 즉, 각 꼭짓점에서의 normal map 을 구하고, 삼각형 내부의 점에서 가중치에 따라 P 점에 있는 normal map 을 계산해 주면 된다! 😁

 

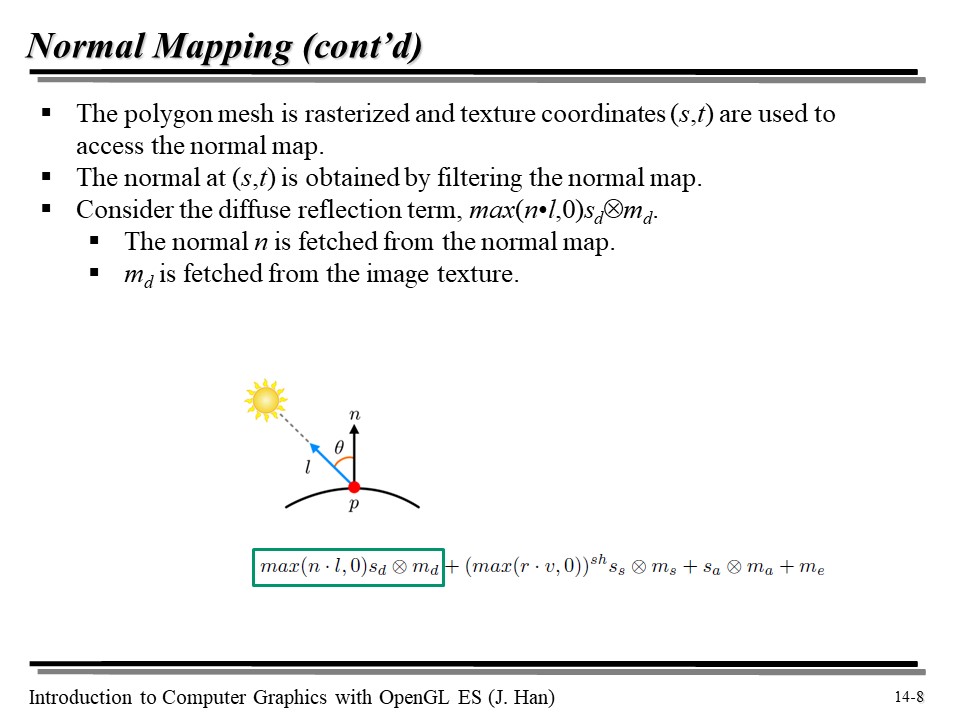
이제 Normal 이 실제로 Lighting 에 어떻게 적용되는지를 살펴보자.

위에서 말하는 Polygon mesh 는 Base surface 를 의미한다. 이때, (s, t) 에서의 normal 은 normal map 에서 bilinear interpolation 을 해 주면 간단히 구할 수 있다. (아까 이전 슬라이드에서 설명했던 내용과 비슷하다)

이때, Phong Lighting Model 을 적용한다고 해 보자. 그럼... n 은 normal map 으로부터 가져올 수 있고, md 는 텍스쳐로부터 가져올 수 있다.

 

Phong Lighting Model 의 실제 코드를 보자. Vertex Shader 의 3대(?) 구성요소인 Position, Normal, Texture Coordinate 이 보인다.

Rasterizer 는 p1, p2 사이의 점 a, b 에 대한 Normal 을 계산해 준 후, Fragment Shader 로 넘길 것이다... 😃

 

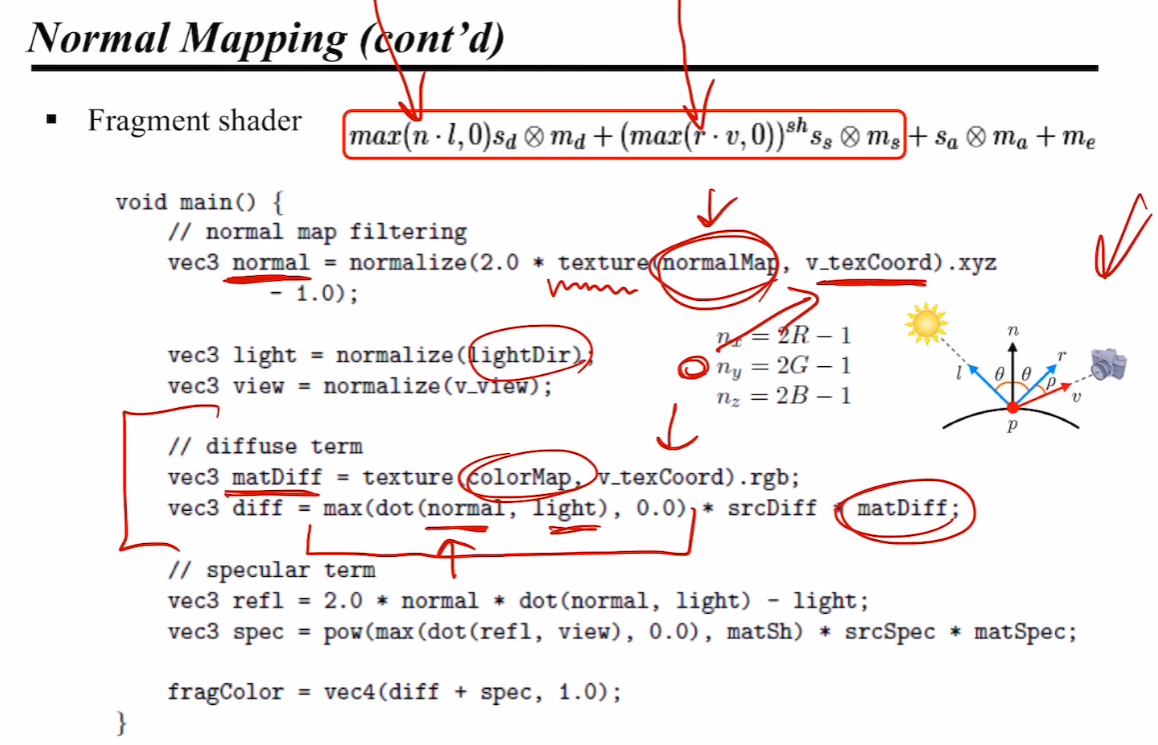
Fragment Shader 는 공식에 맞게 계산만 해주면 된다! 😊

 

Normal Map 을 사용하는지 여부는... 보면 퀄리티에 상당한 차이가 있다는 것을 알 수 있다 😂

 

 

Tangent-Space Normal Mapping

위 그림은 우리가 그린 노말 맵을 가시화한 것이다! 오른쪽에는 구부러진 녀석들의 노말 맵이다.

그런데 끝 점은 왜 아래와 같이 자연스럽게 나올까...?

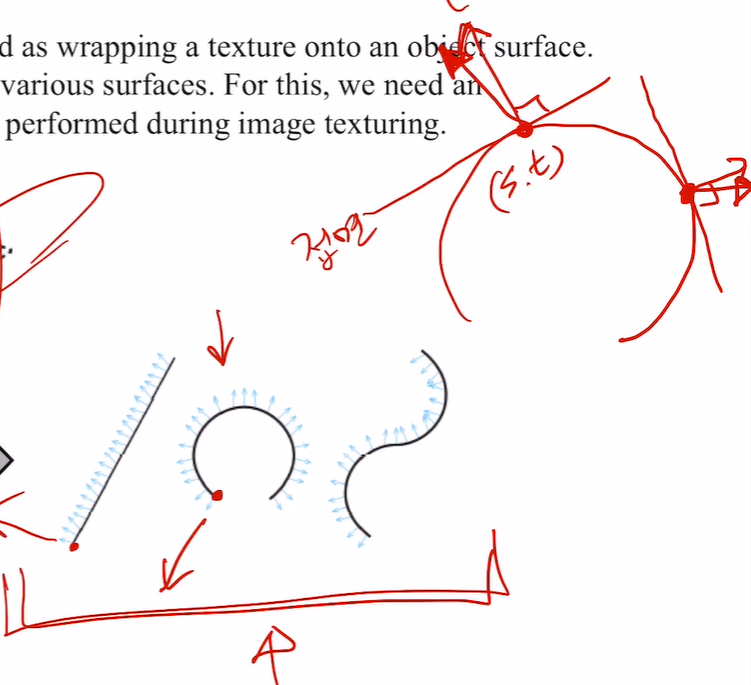
끝 점에서는 다른 방식을 사용해야 할 것처럼도 보이는데.. 사실 접선을 그려서 노말 벡터를 얻을 수도 있다! 😃

 

표면 위의 한 점에 대한 tangent space 는 T, B, N 3 개의 orthonormal 한 벡터로 이루어진다. 

노말 매핑을 사용하지 않는다고 하면, Np 를 라이팅에 사용하면 된다. 해당 벡터는 당연히 (0, 0, 1) 이 될 것이다. 그런데 우리는 노말 매핑에서 갖고 온

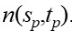
위 녀석을 사용할 것이다. 그런데, 이 녀석이 Np 를 대체하니까... 사실, 이 녀석은 탄젠트 공간 위에 정의된 녀석이라고 간주할 수 있다! 😮

normal 과 light 의 내적을 취한다고 해 보자. 근데 normal 은 Tangent 공간에서, light 은 World 공간에서 정의되어 있다. 그래서 이게 되면 안되는데...

위의 예에서 이게 가능했던 이유는, World Space 의 basis(x, y, z)  와 Tangent Space 의 basis(T, B, N) 이 우연찮게도 같아서 가능했던 것이다 😅 그럼 이 내적이 항상 성립하려면.. 변환이 필요할 것이다!

 

우리는 전처리 단계에서 T, B, N 을 만들고, Vertex Shader 에게 넘겨줄 수 있다. 이는 추후 Space 변환을 위해 사용될 것이다...

 

자, 그럼 Vertex Array 에 T, B, N 이 있으니까, 이 녀석들을 World Space 로 변환할 수 있다. 이는 World Space 에서의 light vector 를 tangent space 로 옮길 수 있는 회전 행렬을 만들 수 있다는 것을 의미한다 😆

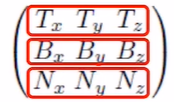
이 페이지가 .. 가장 중요한 슬라이드다! 😄

 

자, 이제 코드를 보자. lightDir 가 바로 빛 벡터이고, 해당 벡터를 tangent space 로 바꿀 것이다.

Nor, Tan 은 World Space 에서의 N 과 T 벡터이다. (Bin 은 B 로, 외적을 해서 구할 수 있다)

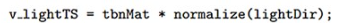
위 식이 light 벡터를 Tangent Space 로 바꿔주는 식이다. 😉

 

위 식처럼... lighting 에 쓰일 벡터들을 Tangent Space 로 변환할 수 있다!

 

위가 그 결과값이다 😊

 

(a) 는 저해상도 모델, (e) 는 고해상도 모델이다.

 

이 부분은 관심이 있으면 따로 찾아보도록 하자 😅

 

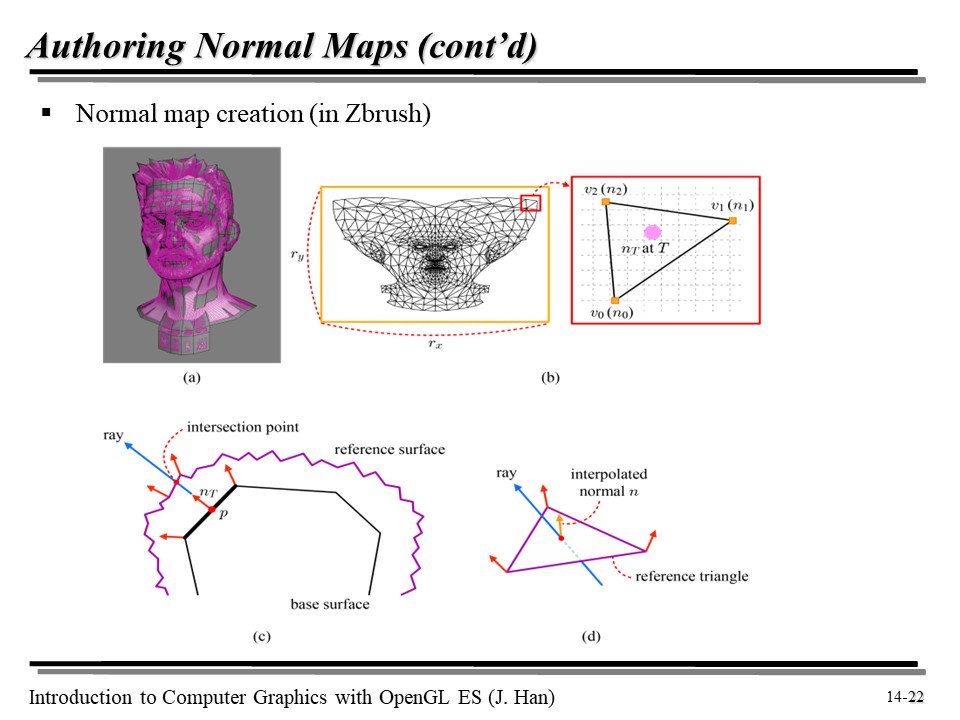
이것도!