[OpenGL ES] 13강 : 스켈레톤(Skeleton), Bone Space, Skinning, Forward Kinematics, Inverse Kinematics

이 강의는 유투브에 무료로 공개되어 있는 한정현 교수님의 컴퓨터 그래픽스 강좌를 정리한 글입니다. 자세한 내용은 강의를 직접 들으시거나 책을 구입하셔서 확인해 보세요. 강의 자료는 깃헙 링크에 올라와 있습니다.

---

요약 :

1. 캐릭터 애니메이션을 구현할 때는 일반적으로 스켈레톤을 많이 사용한다. 각 뼈는 서로 부모 자식 관계를 맺고 있으며 뼈에 있는 각 vertex 는 해당 뼈의  Bone Space 에 정의된 좌표를 가질 수 있다.

2. Forward Kinematics 는 Skeleton 의 Hierarchy 에서 부모로부터 자식까지, Top-Down traversal 방식으로 움직임을 적용하는 방식이다. 각 뼈가 독립적으로 움직인다고 가정하고, 해당 Bone Space 에서 Character Space 까지 변환 행렬을 곱해나가면 된다!

3. Inverse Kinematics 는 끝 점부터 시작하여 Bone 의 위치와 회전을 해석학적으로 결정하는 방식이다. 목표 지점의 끝 Bone 부터 시작하여 회전 및 translation 을 iterative 하게 적용하면 된다.

스켈레톤 (Skeleton)

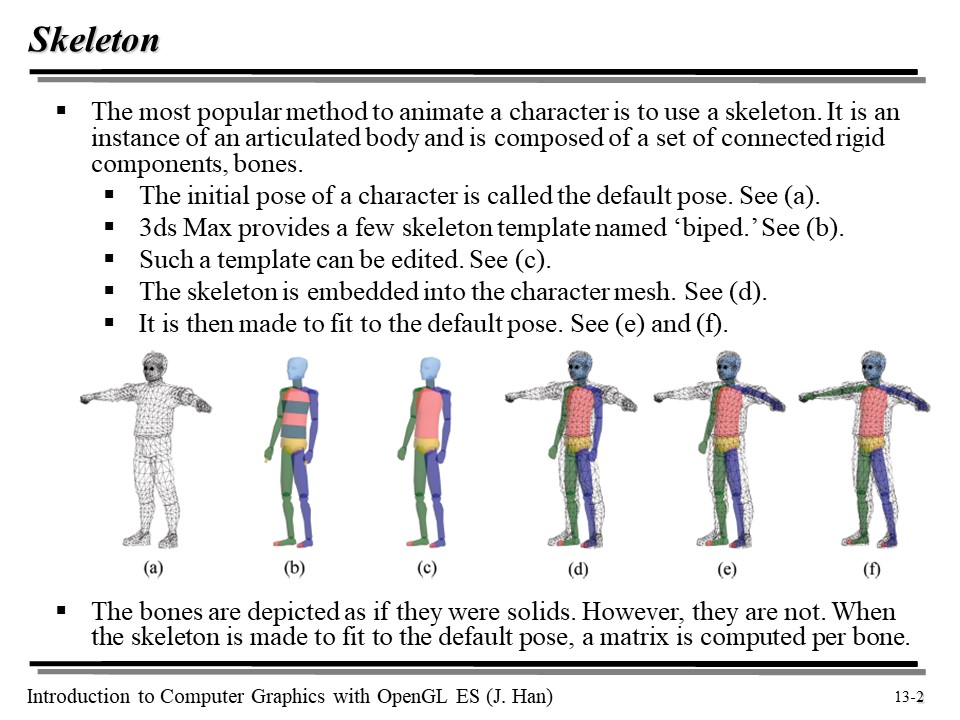
캐릭터 애니메이션을 만드는 제일 쉬운 방법은 스켈레톤을 사용하는 것이다. 위의 그림을 보면 각 단계마다 스켈레톤을 어떻게 처리하는지 보여준다.

뼈는 마치 고체인것 처럼 묘사되지만, 사실은 그렇지 않다. 스켈레톤이 기본 포즈에 맞도록 만들어질때, 뼈마다 행렬이 생성된다. 이는 뼈가 관절을 통해 동적으로 움직일 수 있다는 것이다.

 

위는 일반적으로 사용하는 스켈레톤의 계층 구조이다. 부모의 회전은 그 아래 자손들에게도 영향을 미친다!

 

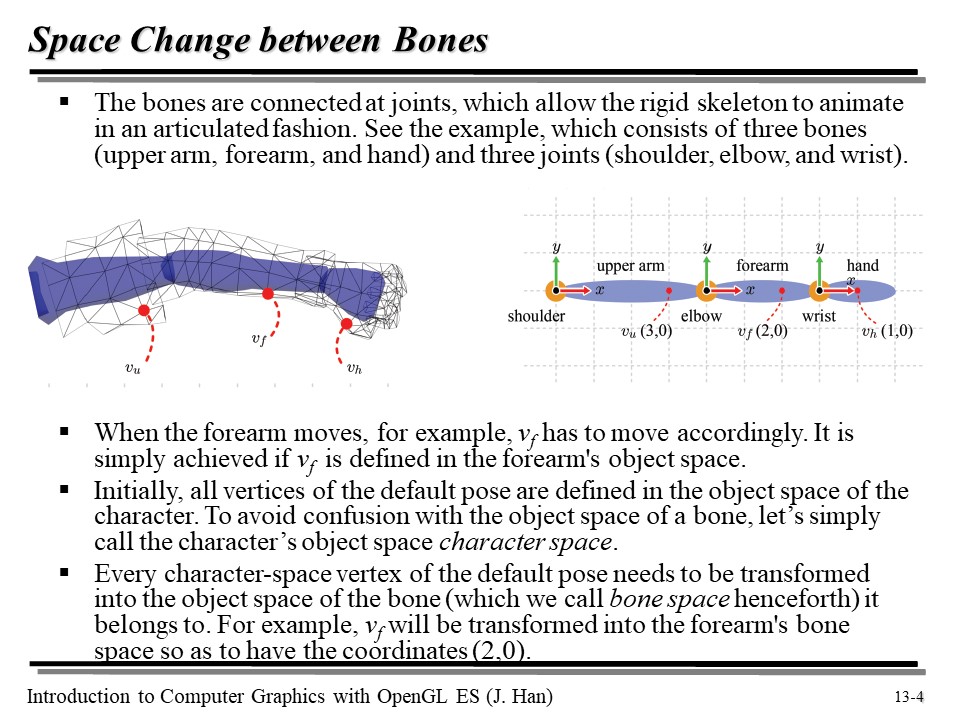
u, f, h 는 각각 upper arm, forearm, hand 에 있는 점을 나타낸다. 각각의 뼈도 joint 를 원점으로 하는 좌표계를 가질 수 있는데... 그 그림이 다음과 같이 잘 나와있다.

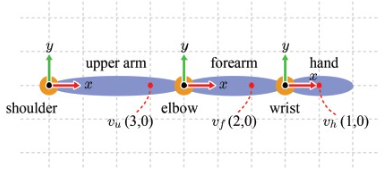
즉 forearm 이 움직이면, vf 점도 같이 이동할 것이다.

그런데 사실 우리는 기본 포즈에서의 각 점이 캐릭터의 오브젝트 공간(Character's Object Space)에 정의되어 있었다. 그런데 애니메이션을 표현하기 위해, 각 점을 이제 각 뼈에 해당하는 공간 좌표계인 Bone Space 로 변환할 것이다. 즉, vf 가 (2, 0) 으로 표현되었는데, 이는 Bone Space 에서의 좌표를 의미한다! 😄

 

그럼 이제 다시 Bone Space 에서 Character Space 로의 변환을 생각해 보자. 이때 사용하는 행렬은 Character Space 에서 Bone Space 로의 변환 행렬의 inverse 일 것이다.

일단 forearm 을 부모 뼈의 공간으로 좌표 변환해보자... forearm 에 있는 vf 점을 upper arm 공간으로 바꾸면 아래와 같이 나온다(여기서는 translation 만 하면 된다).

그럼 손에 있는 vh 점을 upper arm 공간으로 변환할 수 있을까?

물론 간단히 할 수 있다! 그냥 부모로의 변환을 2번 해주면 된다 😆 즉, hand 를 forearm 으로 옮기고, forearm 에서 다시 upperarm 으로 이동하는 것이다.

 

즉, 우리는 Bone Space 에서 Parent 로 변환을 할 때, 부모 행렬을 곱해주기만 하면 된다는 것을 알 수 있다. 거꾸로 올라가면 되는 일이라, 정말 간단히 표현할 수 있다.

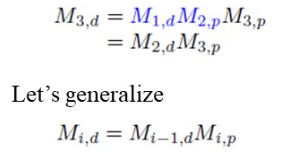
이런 식으로 올라가다 보면, 우리는 Bone Space 에서 Character Space 로의 변환을 매우 쉽게 계산할 수 있다. 이 예에서는 Pelvis 의 Bone Space 가 Character Space 와 동일하다고 가정했다. 😊

 

그런데 Character Space 에서 Bone Space 로 이동하려면.. 이전에 곱해줬던 M 행렬들의 역행렬을 취해줘야 한다. 우리는 top-down traversal 을 위한 행렬을 간단히 구할 수 있다.

 

 

순운동학(Foward Kinematics)

각 뼈들은 독자적으로 움직인다. 위 예에서는 forearm 이 90도 회전한 그림을 보여주고 있는데, 이것을 어떻게 렌더링할 수 있을까?

일단 각 Bone Space 에서 정의된 Vertices 는 Character Space 로 변환되어야 한다(Character Space 가 Object Space 임). 즉, 위에서 forearm 에 있는 v5 점을 어떻게 Character Space 로 변환하는지가 핵심인 것이다.

그것을 변환하는 행렬을 M(5, a) 라고 하자.

 

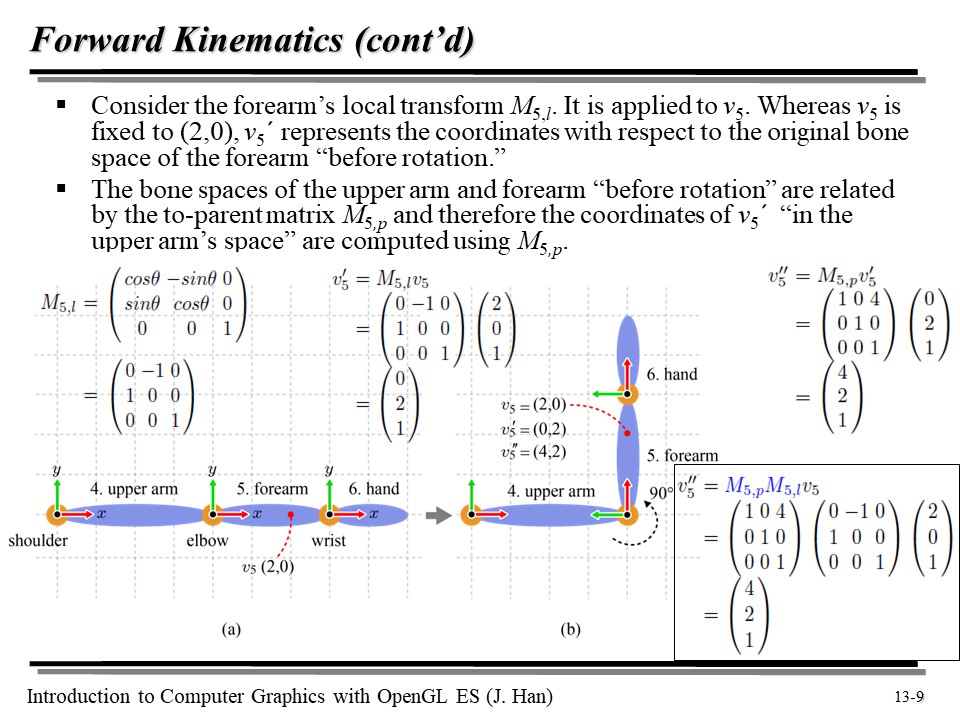
forearm 의 local transform M(5, l) 을 보자(지역변환이라고도 한다).

이 녀석이 v5 에 적용되어 v5' 가 만들어 지는데... 여기에 M(5, p) 를 곱해서, forearm 의 Bone Space 에 정의된 좌표를 upperarm 의 Bone Space 에서의 좌표로 변환해 줄 수 있다.

 

그럼 이 녀석을 어떻게 Character Space 로 보낼까? 그냥 해왔던 대로... 부모 공간으로의 변환 행렬 M 을 곱해주면 된다!

점화식도 너무 간단하다 :

 

뭐... 참고로 읽어보자.

 

즉, 위의 야구선수의 각 Bone 에 있는 점은, 각 뼈에서 움직인 후, Character Space 로 변환되어 animated pose 가 만들어질 것이다! 😉

 

 

Skinning

그런데 사실 피부와 뼈는 일대일 대응관계가 아니다.. upper arm 에 있는 피부는, forearm 에 있는 뼈의 움직임에 영향을 받는다 😅 (뼈 위에 있는 점 a, b, c 를 보면, 뼈가 굽어졌을 때, 보간이 필요하다는 것을 확실히 알게 해 준다)

a, b, c 는 각 뼈에 정의된 점이다. 그런데 a 의 경우, upper arm 에서 좌표를 정의할 수도 있고, forearm 에서 좌표를 정의할 수도 있다(왜냐면 걸쳐 있으니까). 한 점이 각 뼈와 얼마나 가까이 있는지를 아래와 같이 표로 정의하고,

각 뼈에서의 상대적 위치를 왼쪽 그림과 같이 쓴 다음, 가중치를 이용해 보간하면 적절한 점 a', b', c' 가 나온다! 😁

 

이제 실제 예시를 보자. 한 점 v 를 각각 forearm 과 hand 에서 v5 와 v6 로 정의하고 있다.

위 식에서 첫 항은 forearm 을 기준으로 계산된 것을, 둘째 항은 hand 를 기준으로 계산된 결과를 보여준다. 그런데 실제 한 점 은 뼈 2 개가 아니라 (거의) 모든 뼈에 대해 좌표를 계산할 수 있으므로, 아래와 같이 표현할 수도 있다!

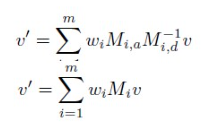
물론 '모든' 뼈에 대한 건 아니고, 실제로 영향을 주는 뼈 갯수는 어느 정도 정해져 있을 것이다! 😅

 

실제로, m 의 갯수 (한 점에 영향을 주는 뼈의 갯수)는 일반적으로 4 정도로 제한된다. 모든 뼈에 대해 행렬식을 계산을 해야 한다고 하면 일이 매우 복잡해질 것이다.. 🙂

Skinning 알고리즘은 일반적으로 vertex shader 에 의해 구현된다. 이때 matrix pallete 는 uniform 으로 들어갈 것이다!

 

지금껏 배운 내용을 정리하면 위의 슬라이드가 될 것이다 😄

 

실제 키프레임을 이용해 중간 프레임을 생성하는 과정은 위와 같다.

 

역운동학 (Inverse Kinematics)

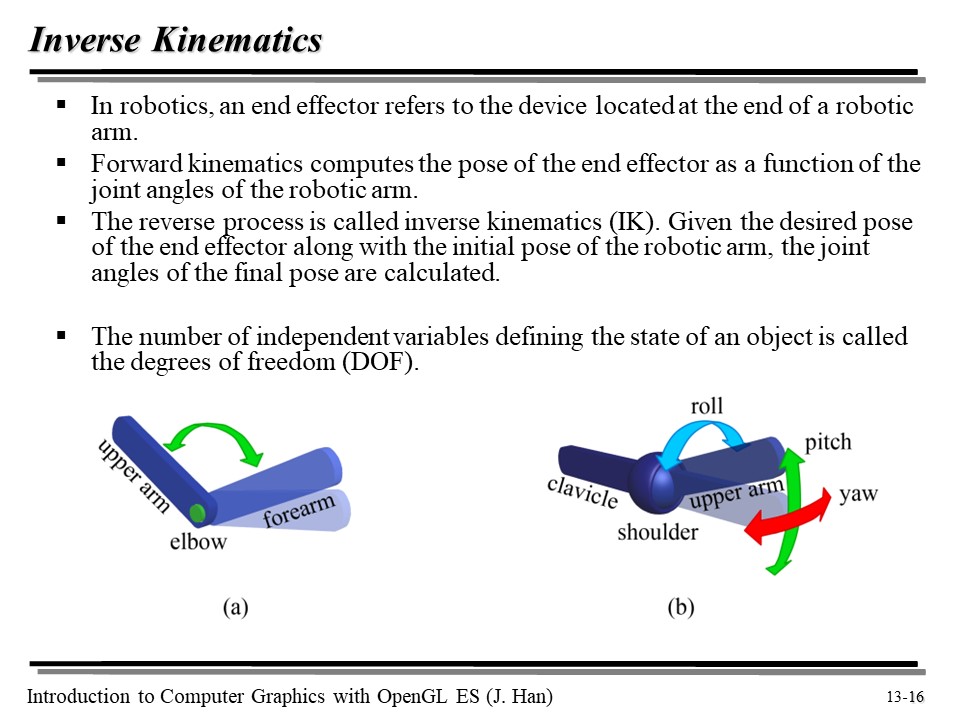
로봇 공학에서, end effector 는 로봇 팔의 끝에 위치한 device 를 의미한다. Forward kinematics 는 로봇 팔의 joint angle 의 함수로 end effector 의 포즈를 계산한다.

그 역순의 프로세스가 inverse kinematics(IK) 이다. 즉, 로봇 팔의 초기 포즈와 결과값에 해당하는 end effector 의 포즈가 주어졌을 때, 최종 포즈에서의 joint angle 을 계산하는 방식이다.

일단 DOF(Degree of Freedom) 이라는 개념이 있는데, 이는 오브젝트의 상태를 표현할 때 필요한 변수의 갯수를 의미한다. (a) 의 경우 1, (b) 의 경우 3이 될 것이다.

 

Inverse Kinematics 의 해석적인 기법을 한 번 보자.

최종 결과값에서... 로봇 팔의 끝 점이 G 를 터치한다고 가정하자. 일단 제 2 코사인 법칙을 쓰면 𝛉 각을 구할 수 있다(팔의 길이는 일정하고, 대각선 길이는 점과 점 사이의 거리로 구함).

사실 우리가 할 일은 간단한데, 기존의 T 점에서 G 점으로 팔을 이동시킬 때... v1 벡터를 v2 에 일치시도록 회전하면 된다. 이건... Arcball 에서 했던 것과 동일하다! 회전축은 그냥 v1 x v2 가 될 것이다 😉

 

실제로는, CCD(Cyclic Coordinate Descent) 방식을 이용해서 iterative 하게 각도를 계산한다.

먼저, 제일 끝 bone 부터 목표 지점과 조금씩 맞추어 나간다. 그림으로 보면 그 원리를 명확히 이해할 수 있다! 😎

 

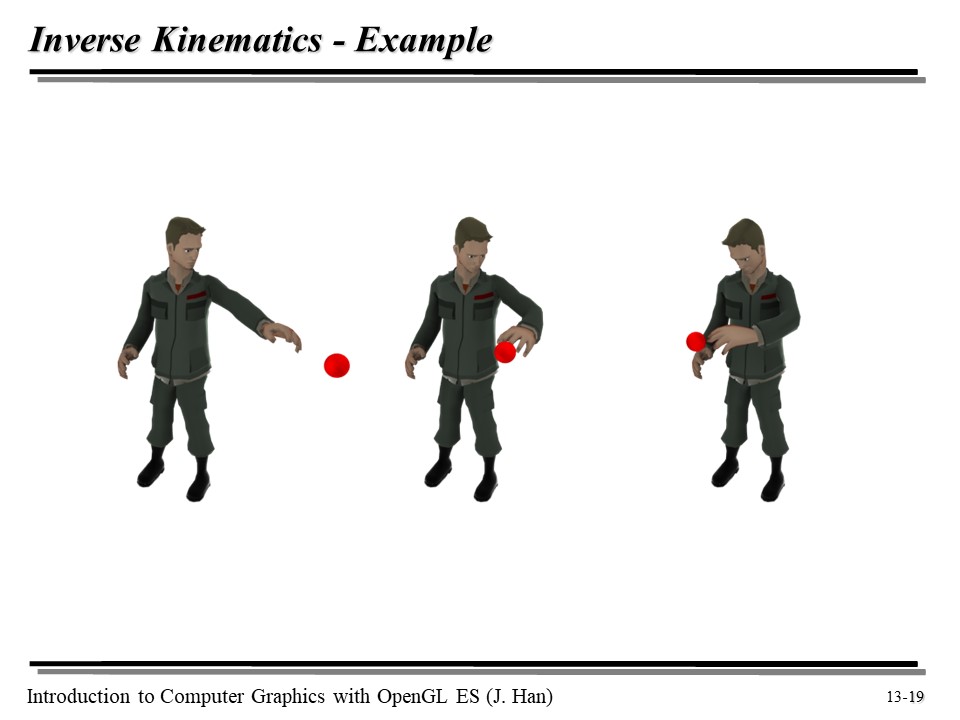
위는 Inverse Kinematics 를 적용한 결과를 잘 보여준다. 게임에서는 실제로 IK 를 많이 사용한다 🙃