Solutions to Linear Algebra, Stephen H. Friedberg, Fourth Edition (Chapter 7)

Solution maual to Linear Algebra, Fourth Edition, Stephen H. Friedberg. (Chapter 7)

Solutions to Linear Algebra, Fourth Edition, Stephen H. Friedberg. (Chapter 7)

Linear Algebra solution manual, Fourth Edition, Stephen H. Friedberg. (Chapter 7)

Linear Algebra solutions Friedberg. (Chapter 7)

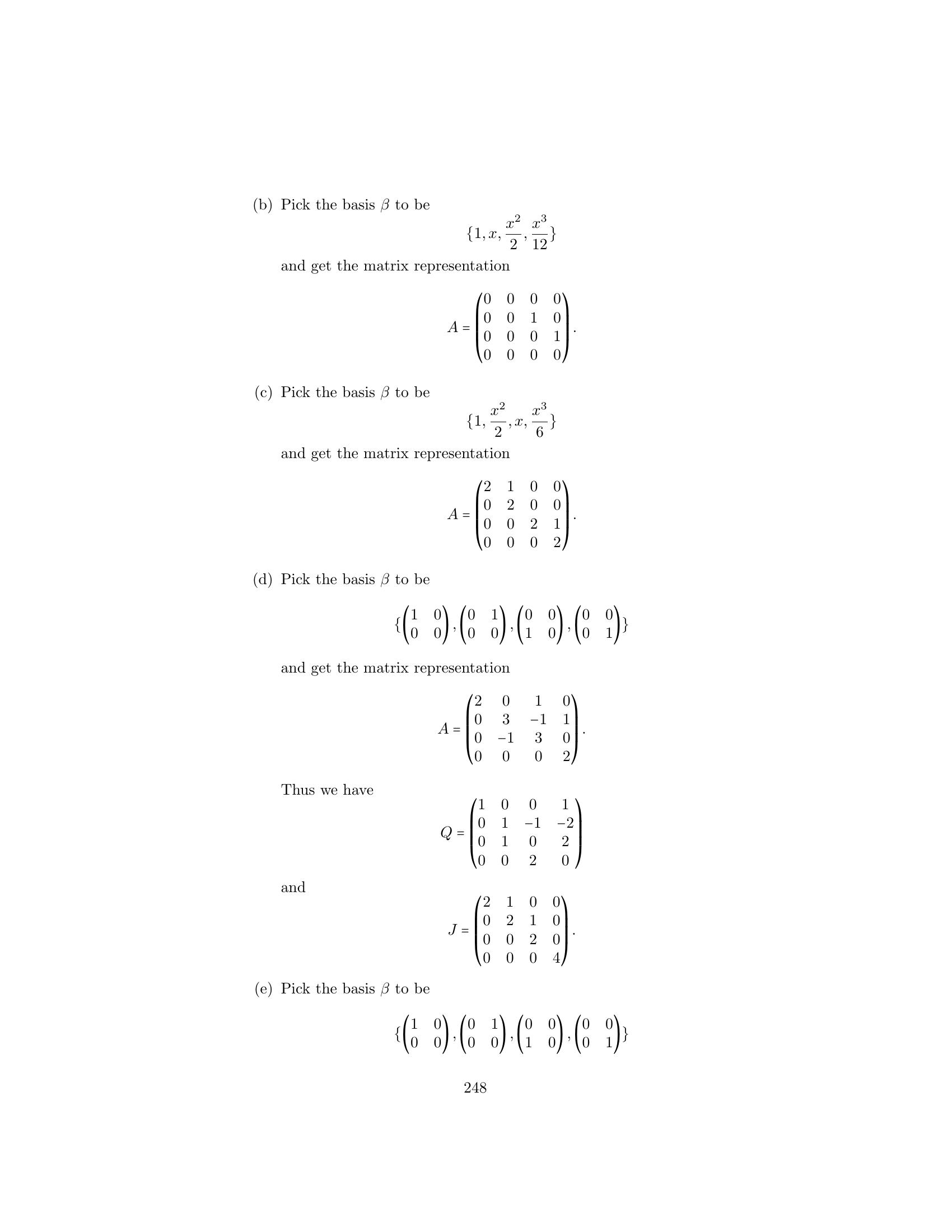
1.Label(a)(b)(c)(d)(e)(f )(g)(h)the following statements as true or false. Eigenvectors of a linear operator T are also generalized eigenvec- tors of T. It is possible for a generalized eigenvector of a linear operator T to correspond to a scalar that is not an eigenvalue of T. Any linear operator on a finite-dimensional vector space has a Jor- dan canonical form. A cycle of generalized eigenvectors is linearly independent. There is exactly one cycle of generalized eigenvectors correspond- ing to each eigenvalue of a linear operator on a finite-dimensional vector space. Let T be a linear operator on a finite-dimensional vector space whose characteristic polynomial splits, and let λ1 , λ2 , . . . , λk be the distinct eigenvalues of T. If, for each i, βi is a basis for Kλi , then β1 ∪ β2 ∪ · · · ∪ βk is a Jordan canonical basis for T. For any Jordan block J, the operator LJ has Jordan canonical form J. Let T be a linear operator on an n-dimensional vector space whose characteristic polynomial splits. Then, for any eigenvalue λ of T, Kλ = N((T − λI)n ). Sec. 7.1 The Jordan Canonical Form I 495 2. For each matrix A, find a basis for each generalized eigenspace of LA consisting of a union of disjoint cycles of generalized eigenvectors. Then find a Jordan canonical form J of A.   1 1 1 2 (a) A = (b) A = −1 3 3 2 ⎛ ⎞ ⎛ ⎞ 2 1 0 0 11 −4 −5 ⎜0 2 1 0⎟ (c) A = ⎝21 −8 −11⎠ (d) A = ⎜ ⎟ ⎝0 0 3 0⎠ 3 −1 0 0 1 −1 3 3. For each linear operator T, find a basis for each generalized eigenspace of T consisting of a union of disjoint cycles of generalized eigenvectors. Then find a Jordan canonical form J of T. (a) T is the linear operator on P2 (R) defined by T(f (x)) = 2f (x) − f  (x) (b) V is the real vector space of functions spanned by the set of real valued functions {1, t, t2 , et , tet }, and T is the linear operator on V defined by T(f ) = f  .  1 1 (c) T is the linear operator on M2×2 (R) defined by T(A) = · A 0 1 for all A ∈ M2×2 (R). (d) T(A) = 2A + At for all A ∈ M2×2 (R). 4. † Let T be a linear operator on a vector space V, and let γ be a cycle of generalized eigenvectors that corresponds to the eigenvalue λ. Prove that span(γ) is a T-invariant subspace of V. 5.Let γ1 , γ2 , . . . , γp be cycles of generalized eigenvectors of a linear op- erator T corresponding to an eigenvalue λ. Prove that if the initial eigenvectors are distinct, then the cycles are disjoint. 6.Let T : V → W be a linear transformation. Prove the following results. (a) N(T) = N(−T). (b) N(Tk ) = N((−T)k ). (c) If V = W (so that T is a linear operator on V) and λ is an eigen- value of T, then for any positive integer k 7.N((T − λIV )k ) = N((λIV − T)k ). Let U be a linear operator on a finite-dimensional vector space V. Prove the following results. (a) N(U) ⊆ N(U2 ) ⊆ · · · ⊆ N(U k ) ⊆ N(Uk+1 ) ⊆ · · · . 496 Chap. 7 Canonical Forms (b)(c)(d)(e)(f )If rank(Um ) = rank(Um+1 ) for some positive integer m, then rank(Um ) = rank(Uk ) for any positive integer k ≥ m. If rank(Um ) = rank(Um+1 ) for some positive integer m, then N(Um ) = N(Uk ) for any positive integer k ≥ m. Let T be a linear operator on V, and let λ be an eigenvalue of T. Prove that if rank((T−λI)m ) = rank((T−λI)m+1 ) for some integer m, then Kλ = N((T − λI)m ). Second Test for Diagonalizability. Let T be a linear operator on V whose characteristic polynomial splits, and let λ1 , λ 2 , . . . , λk be the distinct eigenvalues of T. Then T is diagonalizable if and only if rank(T − λI) = rank((T − λI)2 ) for 1 ≤ i ≤ k. Use (e) to obtain a simpler proof of Exercise 24 of Section 5.4: If T is a diagonalizable linear operator on a finite-dimensional vec- tor space V and W is a T-invariant subspace of V, then TW is diagonalizable. 8.Use Theorem 7.4 to prove that the vectors v1 , v2 , . . . , vk in the statement of Theorem 7.3 are unique. 9.Let T be a linear operator on a finite-dimensional vector space V whose characteristic polynomial splits. (a) Prove Theorem 7.5(b). (b) Suppose that β is a Jordan canonical basis for T, and let λ be an eigenvalue of T. Let β  = β ∩ Kλ . Prove that β  is a basis for Kλ . 10.11.Let T be a linear operator on a finite-dimensional vector space whose characteristic polynomial splits, and let λ be an eigenvalue of T. (a)(b)Suppose that γ is a basis for Kλ consisting of the union of q disjoint cycles of generalized eigenvectors. Prove that q ≤ dim(Eλ ). Let β be a Jordan canonical basis for T, and suppose that J = [T]β has q Jordan blocks with λ in the diagonal positions. Prove that q ≤ dim(Eλ ). Prove Corollary 2 to Theorem 7.7. Exercises 12 and 13 are concerned with direct sums of matrices, defined in Section 5.4 on page 320. 12. Prove Theorem 7.8. 13.Let T be a linear operator on a finite-dimensional vector space V such that the characteristic polynomial of T splits, and let λ1 , λ2 , . . . , λk be the distinct eigenvalues of T. For each i, let Ji be the Jordan canonical form of the restriction of T to Kλi . Prove that J = J1 ⊕ J2 ⊕ · · · ⊕ Jk is the Jordan canonical form of J. 1.Label the following statements as true or false. Assume that the char- acteristic polynomial of the matrix or linear operator splits. (a) The Jordan canonical form of a diagonal matrix is the matrix itself. (b) Let T be a linear operator on a finite-dimensional vector space V that has a Jordan canonical form J. If β is any basis for V, then the Jordan canonical form of [T]β is J. (c) Linear operators having the same characteristic polynomial are similar. (d) Matrices having the same Jordan canonical form are similar. (e) Every matrix is similar to its Jordan canonical form. (f ) Every linear operator with the characteristic polynomial (−1)n (t − λ)n has the same Jordan canonical form. (g) Every linear operator on a finite-dimensional vector space has a unique Jordan canonical basis. (h) The dot diagrams of a linear operator on a finite-dimensional vec- tor space are unique. 510 Chap. 7 Canonical Forms 2. Let T be a linear operator on a finite-dimensional vector space V such that the characteristic polynomial of T splits. Suppose that λ1 = 2, λ2 = 4, and λ3 = −3 are the distinct eigenvalues of T and that the dot diagrams for the restriction of T to Kλi (i = 1, 2, 3) are as follows: λ1 = 2 λ2 = 4 λ3 = −3 • • • • • • • • • • • • Find the Jordan canonical form J of T. 3. Let T be a linear operator on a finite-dimensional vector space V with Jordan canonical form ⎛ ⎞ 2 1 0 0 0 0 0 ⎜ 0 2 1 0 0 0 0 ⎟ ⎜ ⎟ ⎜ 0 0 2 0 0 0 0 ⎟ ⎜ ⎟ ⎜ 0 0 0 2 1 0 0 ⎟ . ⎜ ⎟ ⎜ 0 0 0 0 2 0 0 ⎟ ⎜ ⎟ ⎝ 0 0 0 0 0 3 0 ⎠ 0 0 0 0 0 0 3 (a) (b) (c) (d) (e)Find the characteristic polynomial of T. Find the dot diagram corresponding to each eigenvalue of T. For which eigenvalues λi , if any, does Eλi = Kλi ? For each eigenvalue λi , find the smallest positive integer pi for which K λi = N((T − λi I)pi ). Compute the following numbers for each i, where Ui denotes the restriction of T − λi I to Kλi . (i) rank(Ui ) (ii) rank(U2 ) i(iii) nullity(Ui ) (iv) nullity(U2 ) i4. For each of the matrices A that follow, find a Jordan canonical form J and an invertible matrix Q such that J = Q−1 AQ. Notice that the matrices in (a), (b), and (c) are those used in Example 5. ⎛ ⎞ ⎛ ⎞ −3 3 −2 0 1 −1 (a) A = ⎝−7 6 −3⎠ (b) A = ⎝−4 4 −2⎠ 1 −1 2 −2 1 1 ⎛ ⎞ ⎛ ⎞ 0 −3 1 2 (c) A = ⎝−3 0 −1 −1 −2⎠ −1 (d) A = ⎜ ⎜−2 1 −1 2⎟ ⎟ ⎝−2 1 −1 2⎠ 7 5 6 −2 −3 1 4 Sec. 7.2 The Jordan Canonical Form II 511 5.For each linear operator T, find a Jordan canonical form J of T and a Jordan canonical basis β for T. (a) V is the real vector space of functions spanned by the set of real- valued functions {et , tet , t2 et , e2t }, and T is the linear operator on V defined by T(f ) = f . (b) T is the linear operator on P3 (R) defined by T(f (x)) = xf (x). (c) T is the linear operator on P3 (R) defined by T(f (x)) = f (x) + 2f (x). (d) T is the linear operator on M2×2 (R) defined by  3 1 T(A) = · A − At . 0 3 (e)T is the linear operator on M2×2 (R) defined by  3 1 T(A) = · (A − At ). 0 3 (f )V is the vector space of polynomial functions in two real variables x and y of degree at most 2, as defined in Example 4, and T is the linear operator on V defined by ∂ ∂ T(f (x, y)) = f (x, y) + f (x, y). ∂x ∂y 6.Let A be an n × n matrix whose characteristic polynomial splits. Prove that A and At have the same Jordan canonical form, and conclude that A and At are similar. Hint: For any eigenvalue λ of A and At and any positive integer r, show that rank((A − λI)r ) = rank((At − λI)r ). 7.Let A be an n × n matrix whose characteristic polynomial splits, γ be a cycle of generalized eigenvectors corresponding to an eigenvalue λ, and W be the subspace spanned by γ. Define γ to be the ordered set obtained from γ by reversing the order of the vectors in γ. t (a) Prove that [TW ]γ  = ([TW ]γ ) . (b) Let J be the Jordan canonical form of A. Use (a) to prove that J and J t are similar. (c) Use (b) to prove that A and At are similar. 8.Let T be a linear operator on a finite-dimensional vector space, and suppose that the characteristic polynomial of T splits. Let β be a Jordan canonical basis for T. (a) Prove that for any nonzero scalar c, {cx : x ∈ β} is a Jordan canon- ical basis for T. 512 Chap. 7 Canonical Forms (b)(c)Suppose that γ is one of the cycles of generalized eigenvectors that forms β, and suppose that γ corresponds to the eigenvalue λ and has length greater than 1. Let x be the end vector of γ, and let y be a nonzero vector in Eλ . Let γ be the ordered set obtained from γ by replacing x by x + y. Prove that γ is a cycle of generalized eigenvectors corresponding to λ, and that if γ replaces γ in the union that defines β, then the new union is also a Jordan canonical basis for T. Apply (b) to obtain a Jordan canonical basis for LA , where A is the matrix given in Example 2, that is different from the basis given in the example. 9.Suppose that a dot diagram has k columns and m rows with pj dots in column j and ri dots in row i. Prove the following results. (a)(b)(c)(d)m = p1 and k = r1 . pj = max {i : ri ≥ j} for 1 ≤ j ≤ k and ri = max {j : pj ≥ i} for 1 ≤ i ≤ m. Hint: Use mathematical induction on m. r1 ≥ r2 ≥ · · · ≥ rm . Deduce that the number of dots in each column of a dot diagram is completely determined by the number of dots in the rows. 10.Let T be a linear operator whose characteristic polynomial splits, and let λ be an eigenvalue of T. (a) Prove that dim(Kλ ) is the sum of the lengths of all the blocks corresponding to λ in the Jordan canonical form of T. (b) Deduce that Eλ = Kλ if and only if all the Jordan blocks corre- sponding to λ are 1 × 1 matrices. The following definitions are used in Exercises 11–19. Definitions. A linear operator T on a vector space V is called nilpotent if Tp = T0 for some positive integer p. An n × n matrix A is called nilpotent if Ap = O for some positive integer p. 11.Let T be a linear operator on a finite-dimensional vector space V, and let β be an ordered basis for V. Prove that T is nilpotent if and only if [T]β is nilpotent. 12.Prove that any square upper triangular matrix with each diagonal entry equal to zero is nilpotent. 13.Let T be a nilpotent operator on an n-dimensional vector space V, and suppose that p is the smallest positive integer for which Tp = T0 . Prove the following results. (a) N(Ti ) ⊆ N(Ti+1 ) for every positive integer i. Sec. 7.2 The Jordan Canonical Form II 513 (b)(c)(d)There is a sequence of ordered bases β1 , β2 , . . . , βp such that βi is a basis for N(Ti ) and βi+1 contains βi for 1 ≤ i ≤ p − 1. Let β = βp be the ordered basis for N(Tp ) = V in (b). Then [T]β is an upper triangular matrix with each diagonal entry equal to zero. The characteristic polynomial of T is (−1)n tn . Hence the charac- teristic polynomial of T splits, and 0 is the only eigenvalue of T. 14.Prove the converse of Exercise 13(d): If T is a linear operator on an n- dimensional vector space V and (−1)n tn is the characteristic polynomial of T, then T is nilpotent. 15.Give an example of a linear operator T on a finite-dimensional vector space such that T is not nilpotent, but zero is the only eigenvalue of T. Characterize all such operators. 16.Let T be a nilpotent linear operator on a finite-dimensional vector space V. Recall from Exercise 13 that λ = 0 is the only eigenvalue of T, and hence V = Kλ . Let β be a Jordan canonical basis for T. Prove that for any positive integer i, if we delete from β the vectors corresponding to the last i dots in each column of a dot diagram of β, the resulting set is a basis for R(Ti ). (If a column of the dot diagram contains fewer than i dots, all the vectors associated with that column are removed from β.) 17.Let T be a linear operator on a finite-dimensional vector space V such that the characteristic polynomial of T splits, and let λ1 , λ2 , . . . , λk be the distinct eigenvalues of T. Let S : V → V be the mapping defined by S(x) = λ1 v1 + λ2 v2 + · · · + λk vk , where, for each i, vi is the unique vector in Kλi such that x = v1 + v2 + · · · + vk . (This unique representation is guaranteed by Theorem 7.3 (p. 486) and Exercise 8 of Section 7.1.) (a) Prove that S is a diagonalizable linear operator on V. (b) Let U = T − S. Prove that U is nilpotent and commutes with S, that is, SU = US. 18.Let T be a linear operator on a finite-dimensional vector space V, and let J be the Jordan canonical form of T. Let D be the diagonal matrix whose diagonal entries are the diagonal entries of J, and let M = J −D. Prove the following results. (a)(b)M is nilpotent. M D = DM . 514 Chap. 7 Canonical Forms (c) If p is the smallest positive integer for which M p = O, then, for any positive integer r < p, r r−1 r(r − 1) r−2 2 r−1 rJ = Dr + rD M + D M + · · · + rDM + M , 2! and, for any positive integer r ≥ p, r r−1 r(r − 1) r−2 2 J = Dr + rD M + D M + ··· 2! r! r−p+1 p−1+ D M . (r − p + 1)!(p − 1)! 19. Let ⎛ ⎞ λ 1 0 ··· 0 ⎜ ⎜ 0 λ 1 ··· 0 ⎟ ⎟ ⎜ ⎜ 0 0 λ ··· 0 ⎟ ⎟ J = ⎜ ⎜ . .. .. . .. . .. . ⎟ ⎟ ⎜ ⎟ ⎝ 0 0 0 · · · 1 ⎠ 0 0 0 ··· λ be the m × m Jordan block corresponding to λ, and let N = J − λIm . Prove the following results: (a) N m = O, and for 1 ≤ r < m,  1 if j = i + r r Nij = 0 otherwise. (b) For any integer r ≥ m, ⎛ ⎞ r(r − 1) r−2 r(r − 1) · · · (r − m + 2) r−m+1 ⎜ λr rλr−1 λ ··· λ ⎟ ⎜ 2! (m − 1)! ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ r(r − 1) · · · (r − m + 3) ⎟ r ⎜ 0 λr rλr−1 · · · λr−m+2 ⎟ J = ⎜ (m − 2)! ⎟. ⎜ ⎟ ⎜ . . ⎟ ⎜ ⎜ .. .. .. . .. . ⎟ ⎟ ⎝ ⎠ 0 0 0 ··· λr (c) lim J r exists if and only if one of the following holds: r→∞ (i) |λ| < 1. (ii) λ = 1 and m = 1. Sec. 7.2 The Jordan Canonical Form II 515 (Note that lim λr exists under these conditions. See the discus- r→∞ r sion preceding Theorem 5.13 on page 285.) Furthermore, lim Jr→∞ is the zero matrix if condition (i) holds and is the 1 × 1 matrix (1) if condition (ii) holds. (d) Prove Theorem 5.13 on page 285. The following definition is used in Exercises 20 and 21. Definition.For any A ∈ Mn×n(C), define the norm of A by A = max {|Aij | : 1 ≤ i, j ≤ n}. 20.Let A, B ∈ Mn×n (C). Prove the following results. (a) A ≥ 0 and A = 0 if and only if A = O. (b) cA = |c|· A for any scalar c. (c) A + B ≤ A + B. (d) AB ≤ nAB. 21.Let A ∈ Mn×n (C) be a transition matrix. (See Section 5.3.) Since C is an algebraically closed field, A has a Jordan canonical form J to which A is similar. Let P be an invertible matrix such that P −1 AP = J. Prove the following results. (a) Am  ≤ 1 for every positive integer m. (b) There exists a positive number c such that J m  ≤ c for every positive integer m. (c) Each Jordan block of J corresponding to the eigenvalue λ = 1 is a 1 × 1 matrix. (d) lim Am exists if and only if 1 is the only eigenvalue of A with m→∞ absolute value 1. (e) Theorem 5.20(a) using (c) and Theorem 5.19. The next exercise requires knowledge of absolutely convergent series as well as the definition of eA for a matrix A. (See page 312.) 22.23.Use Exercise 20(d) to prove that eA exists for every A ∈ Mn×n (C). Let x = Ax be a system of n linear differential equations, where x is an n-tuple of differentiable functions x1 (t), x2 (t), . . . , x n (t) of the real variable t, and A is an n × n coefficient matrix as in Exercise 15 of Section 5.2. In contrast to that exercise, however, do not assume that A is diagonalizable, but assume that the characteristic polynomial of A splits. Let λ1 , λ2 , . . . , λk be the distinct eigenvalues of A. 516 Chap. 7 Canonical Forms (a)(b)Prove that if u is the end vector of a cycle of generalized eigenvec- tors of LA of length p and u corresponds to the eigenvalue λi , then for any polynomial f (t) of degree less than p, the function eλi t [f (t)(A − λiI)p−1 + f  (t)(A − λi I)p−2 + · · · + f (p−1) (t)]u is a solution to the system x = Ax. Prove that the general solution to x = Ax is a sum of the functions of the form given in (a), where the vectors u are the end vectors of the distinct cycles that constitute a fixed Jordan canonical basis for LA . 24. Use Exercise 23 to find the general solution to each of the following sys- tems of linear equations, where x, y, and z are real-valued differentiable functions of the real variable t. x = 2x + y x = 2x + y (a) y  = 2y − z (b) y  = 2y + z  z = 3z z = 2z 1.Label the following statements as true or false. Assume that all vector spaces are finite-dimensional. (a) Every linear operator T has a polynomial p(t) of largest degree for which p(T) = T0 . (b) Every linear operator has a unique minimal polynomial. (c) The characteristic polynomial of a linear operator divides the min- imal polynomial of that operator. (d) The minimal and the characteristic polynomials of any diagonal- izable operator are equal. (e) Let T be a linear operator on an n-dimensional vector space V, p(t) be the minimal polynomial of T, and f (t) be the characteristic polynomial of T. Suppose that f (t) splits. Then f (t) divides [p(t)]n . (f ) The minimal polynomial of a linear operator always has the same degree as the characteristic polynomial of the operator. (g) A linear operator is diagonalizable if its minimal polynomial splits. (h) Let T be a linear operator on a vector space V such that V is a T-cyclic subspace of itself. Then the degree of the minimal poly- nomial of T equals dim(V). (i) Let T be a linear operator on a vector space V such that T has n distinct eigenvalues, where n = dim(V). Then the degree of the minimal polynomial of T equals n. 2. Find the minimal polynomial of each of the following matrices.   2 1 1 1 (a) (b) 1 2 0 1 ⎛ ⎞ ⎛ ⎞ 4 −14 5 3 0 1 (c) ⎝1 −4 2⎠ (d) ⎝ 2 2 2⎠ 1 −6 4 −1 0 1 3.For each linear operator T on V, find the minimal polynomial of T. (a) V = R2 and T(a, b) = (a + b, a − b) (b) V = P2 (R) and T(g(x)) = g (x) + 2g(x) (c) V = P2 (R) and T(f (x)) = −xf  (x) + f  (x) + 2f (x) (d) V = Mn×n (R) and T(A) = At . Hint: Note that T2 = I. 4.Determine which of the matrices and operators in Exercises 2 and 3 are diagonalizable. 5.Describe all linear operators T on R2 such that T is diagonalizable and T3 − 2T2 + T = T0 . Sec. 7.3 The Minimal Polynomial 523 6. Prove Theorem 7.13 and its corollary. 7. Prove the corollary to Theorem 7.14. 8.Let T be a linear operator on a finite-dimensional vector space, and let p(t) be the minimal polynomial of T. Prove the following results. (a) T is invertible if and only if p(0) = 0. (b) If T is invertible and p(t) = tn + an−1 tn−1 + · · · + a1 t + a0 , then 1  n−1  T−1 = − T + an−1 Tn−2 + · · · + a2 T + a1 I . a0 9.Let T be a diagonalizable linear operator on a finite-dimensional vector space V. Prove that V is a T-cyclic subspace if and only if each of the eigenspaces of T is one-dimensional. 10.Let T be a linear operator on a finite-dimensional vector space V, and suppose that W is a T-invariant subspace of V. Prove that the minimal polynomial of TW divides the minimal polynomial of T. 11.Let g(t) be the auxiliary polynomial associated with a homogeneous lin- ear differential equation with constant coefficients (as defined in Section 2.7), and let V denote the solution space of this differential equation. Prove the following results. (a)(b)(c)V is a D-invariant subspace, where D is the differentiation operator on C∞ . The minimal polynomial of DV (the restriction of D to V) is g(t). If the degree of g(t) is n, then the characteristic polynomial of DV is (−1)n g(t). Hint: Use Theorem 2.32 (p. 135) for (b) and (c). 12.Let D be the differentiation operator on P(R), the space of polynomials over R. Prove that there exists no polynomial g(t) for which g(D) = T0 . Hence D has no minimal polynomial. 13.Let T be a linear operator on a finite-dimensional vector space, and suppose that the characteristic polynomial of T splits. Let λ1 , λ2 , . . . , λk be the distinct eigenvalues of T, and for each i let pi be the order of the largest Jordan block corresponding to λi in a Jordan canonical form of T. Prove that the minimal polynomial of T is (t − λ1 )p1 (t − λ2 )p2 · · · (t − λk )pk . The following exercise requires knowledge of direct sums (see Section 5.2). 524 Chap. 7 Canonical Forms 14.Let T be linear operator on a finite-dimensional vector space V, and let W1 and W2 be T-invariant subspaces of V such that V = W1 ⊕ W2 . Suppose that p1 (t) and p2 (t) are the minimal polynomials of TW1 and TW2 , respectively. Prove or disprove that p1 (t)p2 (t) is the minimal polynomial of T. Exercise 15 uses the following definition. Definition. Let T be a linear operator on a finite-dimensional vector space V, and let x be a nonzero vector in V. The polynomial p(t) is called a T-annihilator of x if p(t) is a monic polynomial of least degree for which p(T)(x) = 0 . 15. † Let T be a linear operator on a finite-dimensional vector space V, and let x be a nonzero vector in V. Prove the following results. (a) The vector x has a unique T-annihilator. (b) The T-annihilator of x divides any polynomial g(t) for which g(T) = T0 . (c) If p(t) is the T-annihilator of x and W is the T-cyclic subspace generated by x, then p(t) is the minimal polynomial of TW , and dim(W) equals the degree of p(t). (d) The degree of the T-annihilator of x is 1 if and only if x is an eigenvector of T. 16.T be a linear operator on a finite-dimensional vector space V, and let W1 be a T-invariant subspace of V. Let x ∈ V such that x ∈ / W1 . Prove the following results. (a)(b)(c)(d)There exists a unique monic polynomial g1 (t) of least positive de- gree such that g1 (T)(x) ∈ W1 . If h(t) is a polynomial for which h(T)(x) ∈ W1 , then g1 (t) divides h(t). g1 (t) divides the minimal and the characteristic polynomials of T. Let W2 be a T-invariant subspace of V such that W2 ⊆ W1 , and let g2 (t) be the unique monic polynomial of least degree such that g2 (T)(x) ∈ W2 . Then g1 (t) divides g2 (t). 1.EXERCISES Label the following statements as true or false. (a) Every rational canonical basis for a linear operator T is the union of T-cyclic bases. 546 Chap. 7 Canonical Forms (b) If a basis is the union of T-cyclic bases for a linear operator T, then it is a rational canonical basis for T. (c) There exist square matrices having no rational canonical form. (d) A square matrix is similar to its rational canonical form. (e) For any linear operator T on a finite-dimensional vector space, any irreducible factor of the characteristic polynomial of T divides the minimal polynomial of T. (f ) Let φ(t) be an irreducible monic divisor of the characteristic poly- nomial of a linear operator T. The dots in the diagram used to compute the rational canonical form of the restriction of T to Kφ are in one-to-one correspondence with the vectors in a basis for Kφ . (g) If a matrix has a Jordan canonical form, then its Jordan canonical form and rational canonical form are similar. 2. For each of the following matrices A ∈ Mn×n (F ), find the rational canonical form C of A and a matrix Q ∈ Mn×n (F ) such that Q−1 AQ = C. ⎛ ⎞ 3 1 0  0 −1 (a) A = ⎝ 0 3 1 ⎠ F = R (b) A = F = R 1 −1 0 0 3  0 −1 (c) A = F = C 1 −1 ⎛ ⎞ 0 −7 14 −6 (d) A = ⎜1 ⎜ −4 6 −3⎟ ⎟ F = R ⎝0 −4 9 −4⎠ 0 −4 11 −5 ⎛ ⎞ 0 −4 12 −7 (e) A = ⎜1 ⎜ −1 3 −3⎟ ⎟ F = R ⎝0 −1 6 −4⎠ 0 −1 8 −5 3. For each of the following linear operators T, find the elementary divisors, the rational canonical form C, and a rational canonical basis β. (a) T is the linear operator on P3 (R) defined by T(f (x)) = f (0)x − f  (1). (b) Let S = {sin x, cos x, x sin x, x cos x}, a subset of F(R, R), and let V = span(S). Define T to be the linear operator on V such that T(f ) = f . (c) T is the linear operator on M2×2 (R) defined by Sec. 7.4 The Rational Canonical Form 547  0 1 T(A) = · A. −1 1 (d) Let S = {sin x sin y, sin x cos y, cos x sin y, cos x cos y}, a subset of F(R × R, R), and let V = span(S). Define T to be the linear operator on V such that ∂f (x, y) ∂f (x, y) T(f )(x, y) = + . ∂x ∂y 4.Let T be a linear operator on a finite-dimensional vector space V with minimal polynomial (φ(t))m for some positive integer m. (a) Prove that R(φ(T)) ⊆ N((φ(T))m−1 ). (b) Give an example to show that the subspaces in (a) need not be equal. (c) Prove that the minimal polynomial of the restriction of T to R(φ(T)) equals (φ(t))m−1 . 5.Let T be a linear operator on a finite-dimensional vector space. Prove that the rational canonical form of T is a diagonal matrix if and only if T is diagonalizable. 6.Let T be a linear operator on a finite-dimensional vector space V with characteristic polynomial f (t) = (−1)n φ1 (t)φ2 (t), where φ1 (t) and φ2 (t) are distinct irreducible monic polynomials and n = dim(V). (a) Prove that there exist v1 , v2 ∈ V such that v1 has T-annihilator φ1 (t), v2 has T-annihilator φ2 (t), and βv1 ∪ βv2 is a basis for V. (b) Prove that there is a vector v3 ∈ V with T-annihilator φ1 (t)φ2 (t) such that βv3 is a basis for V. (c) Describe the difference between the matrix representation of T with respect to βv1 ∪ βv2 and the matrix representation of T with respect to βv3 . Thus, to assure the uniqueness of the rational canonical form, we re- quire that the generators of the T-cyclic bases that constitute a rational canonical basis have T-annihilators equal to powers of irreducible monic factors of the characteristic polynomial of T. 7.Let T be a linear operator on a finite-dimensional vector space with minimal polynomial f (t) = (φ1 (t))m1 (φ2 (t))m2 · · · (φk (t))mk , where the φi (t)’s are distinct irreducible monic factors of f (t). Prove that for each i, mi is the number of entries in the first column of the dot diagram for φi (t). 548 Chap. 7 Canonical Forms 8.Let T be a linear operator on a finite-dimensional vector space V. Prove that for any irreducible polynomial φ(t), if φ(T) is not one-to-one, then φ(t) divides the characteristic polynomial of T. Hint: Apply Exercise 15 of Section 7.3. 9.Let V be a vector space and β1 , β2 , . . . , βk be disjoint subsets of V whose union is a basis for V. Now suppose that γ1 , γ2 , . . . , γk are linearly independent subsets of V such that span(γi ) = span(βi ) for all i. Prove that γ1 ∪ γ2 ∪ · · · ∪ γk is also a basis for V. 10.Let T be a linear operator on a finite-dimensional vector space, and suppose that φ(t) is an irreducible monic factor of the characteristic polynomial of T. Prove that if φ(t) is the T-annihilator of vectors x and y, then x ∈ Cy if and only if Cx = Cy . Exercises 11 and 12 are concerned with direct sums. 11. Prove Theorem 7.25. 12. Prove Theorem 7.26.