KoreanFoodie's Study
게임수학 - 극좌표계 본문

이득우님의 '이득우의 게임수학' 책을 보며 좋은 내용을 정리하고 있습니다. 더 자세한 내용이 궁금하시다면, 책을 구매해 직접 읽어보시기를 추천드립니다!
극좌표계
우리는 기본적으로 데카르트 좌표계를 많이 이용하는데, 사실 회전을 할 때마다 x 와 y 의 변화를 매번 계산하는 것은 매우 번거로운 일일 수 있다. 이 경우, 원점으로부터의 거리 r 과 θ 의 두 요소로 구성된 극좌표계(Polar coordinate system) 을 사용할 수 있다.
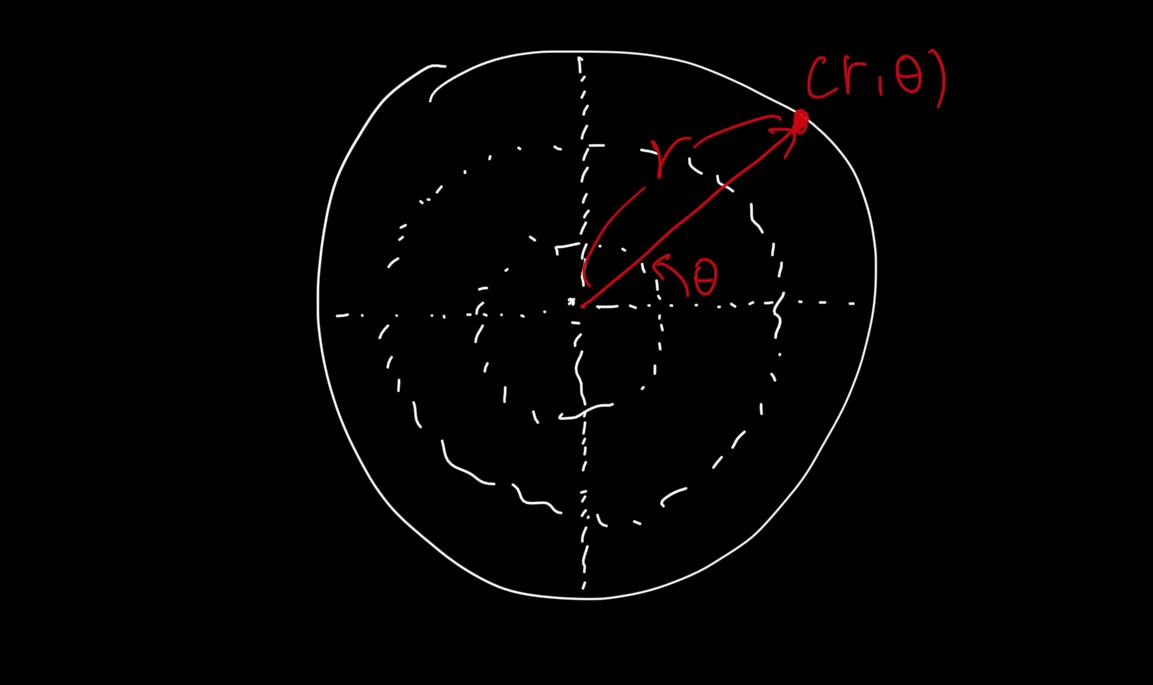
일반적으로 arctan 함수를 이용하면 벡터의 각도를 얻어낼 수 있는데(tanθ = y/x 이므로, θ = arctan(y/x) 이 됨), arctan 함수는 치역이 -180도에서 180도까지 밖에 되지 않는다. 따라서 이를 해결하기 위해, x 와 y 값을 따로 전달하는 arctan 함수인 atan2 함수가 있다. 인자에 y/x 를 한번에 전달하면 해당 벡터가 어떤 사분면에 위치해 있는지 정확히 파악할 수 없지만, atan2 함수는 x 와 y 를 따로 전달하므로 벡터의 각도를 정확히 측정할 수 있다.

극좌표계와 데카르트 좌표계의 변환은 다음과 같이 이루어진다!

'Game Dev > Game Math' 카테고리의 다른 글
| 게임 수학 - 변환 행렬의 역행렬 (0) | 2022.10.29 |
|---|---|
| 게임수학 - 행렬을 이용한 회전변환 (0) | 2022.10.26 |
| 게임수학 - 삼각함수를 활용한 물체의 회전 (0) | 2022.10.23 |
Comments



